4. 与一次函数有关的实际问题

例20 (山东省潍坊课改实验区2007)已知某山区的平均气温与该山的海拔高度的关系见下表：

(1)　　 若海拔高度用x(米)表示，平均气温用y(°C)表示，写出y与x之间的函数关系式；

(2)　　 若某种植物适宜生长在18°C~20°C(包含18°C，也包含20°)的山区，请问该植物适宜种植在海拔为多少米的山区？

例21 (甘肃省2007)甲、乙两人在一次赛跑中，路程s与时间t的关系如图所示(实线为甲的路程与时间的关系图像，虚线为乙的路程与时间的关系图像)，小王根据图像得到如下四个信息，其中错误的是：　　　　　　　　　　　　　　　　　 　　(　　 )

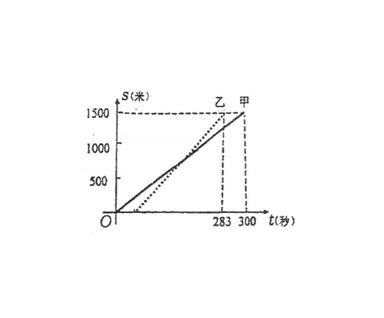　　 (A) 这是一次1500米的赛跑

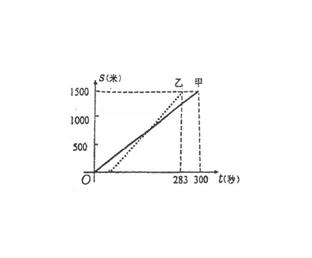(B) 甲、乙两人中先到达终点的是乙

(C) 甲、乙同时起跑

(D) 甲在这次赛跑中的速度为5m/s

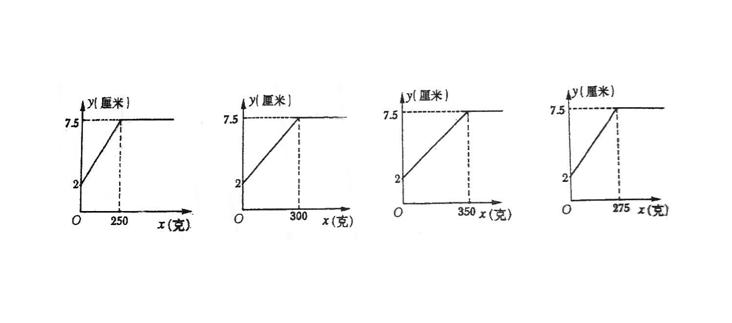例22 (黄冈市2007)某班同学在探究弹簧的长度跟外力的变化关系是，实验记录得到的相应数据如下表：

则y关于x的函数图像是：　　　　　　　　　　　　　　　　　　　　　 (　　 )

　　 (A)　 　　　　　　　　(B)　　　　　　　 (C)　　　　　　　　　 (D)

例23 (1) ★★(沈阳市2007)某市的A县和B县春季育苗，急需化肥分别为90吨和60吨，该市的C县和D县分别储存化肥100吨和50吨，全部调配给A县和B县，已知C、D两县运化肥到A、B两县的运费(元/吨)如下表所示。

出 发 地 运费 目的地	C	D
A	35	40
B	30	45

(1)　　 设C县运到A县的化肥为x吨，求总运费W元与x吨的函数关系式，并写出自变量x的取值范围；

(2)　　 求最低总运费，并说明总运费最低时的运送方案。

3．图形的移动(翻转，平移，旋转)

例18 (四川省含成都市2007)在平面直角坐标系中，直线y=kx+b(k，b为常数，k≠0，b＞0)可以看成是将直线y=kx沿y轴向上平行移动b个单位而得到的，那么将直线y=kx沿x轴向右平行移动m个单位(m＞0)，得到的直线方程是　　　　　 .

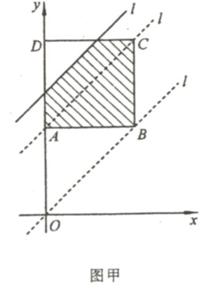
例19 (河南省2007)如图甲，边长为2的正方形ABCD中，顶点A的坐标是(0，2)．一次函数y = x + t的图像l随t的不同取值变化时，位于l的右下方由l和正方形的边围成的图像面积为S(阴影部分)

(1)　　 当t取何值时，S=3

(2)　　 在平面直角坐标系下(如图乙)，画出S与t的图像。

2. 一次函数中的数形结合[用数形结合思想]

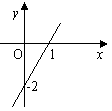例16 (1)(贵阳市课改实验区2007)已知一次函数y=kx+b的图象(如图)，当x＜0时，y的取值范围是

(A)y ＞ 0　　　　　　　 　　(B)y ＜ 0

(C)- 2 ＜ y ＜ 0　　　　　 (D)y ＜ - 2

(2) (福州市2007)已知正比例函数y = kx (k≠0)过第二、四象限，则　 　　　　(　 )

(A)y随x的增大而减小　　　　　　　 (B)y随x的增大而增大

(C)当x＜0时，y随x的增大而增大；当x＞0时，y随x的增大而减小

(D)不论x如何变化，y不变

例17　 新课程标准P36 例11　

　填表并观察下列两个函数的变化情况：

(1)　　 在同一个直角坐标系中画出上面两个函数的图象，比较它们有什么不同；

(2)　　 当 x 从1开始增大时，预测哪一个函数的值先到达100.

1.一次函数的解析式与图象上点的坐标[用方程思想]

(2)(河南省2007) 点M(-2，k)在直线y=2x+1上，M到x轴的距离d=_______．

　 (3)若一次函数图象过A (2, -1)和B两点，其中点B是另一条直线y =﹣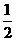x + 3与y 轴的交点，求这个一次函数的解析式.

　 (4) 已知两条直线 y₁ = (m – 1)x + m² – 5 与 y₂ = x – 1的交点恰在y轴上，且y₁随x增大而减小，写出y₁与x之间的函数关系式及此直线与两坐标轴的交点坐标.

　 (5)直线y = kx + b 与直线y = 5﹣4x平行，且与直线y = ﹣3(x﹣6)相交，交点恰在y轴上，求这条直线的函数解析式.

　 (6)直线与x轴交于点A(﹣4，0)，与y轴交于点B，若点B到x轴的距离为2，求这条直线的函数解析式.

　 (7)已知 y = 3x – 2 的图象经过点( a，b )，且 a + b = 6，求a、b的值.

2. 反比例函数中的数形结合(依形判数、由数思形)

例28 (1)反比例函数y=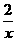的图像在________象限.

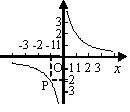
(2)(长沙市2007)反比例函数y=(k≠0)的图象经过点P，如图所示，

根据图象可知，反比例函数的解析式为　　　　　 。

　　　 (A)　　　　　　 (B)　　　　　　　 (C)　　　　　　 (D)

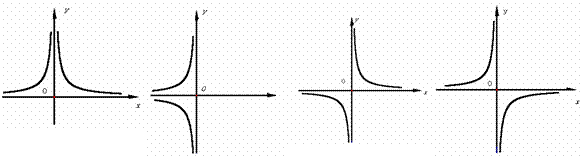
例29　 (南昌市2007年)反比例函数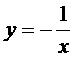的图象大致是上图中的(　 　).

例30 (1)(苏州市2007年) 设有反比例函数 y = 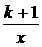，(x₁，y₁)、(x₂，y₂)为其图象上的两点，若 x₁ < 0 < x₂时，y₁ > y₂，则 k 的取值范围是　　　　 .

(由数思形、依形判数)

(2)(山东省潍坊课改实验区2007)若M(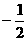，y₁)、N(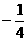，y₂)、P(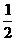，y₃)三点都在函数y=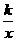(k < 0)的图像上，则y₁ 、y₂ 、y₃ 的大小关系为　　　　　　　　　　　　　　　 　　　　

(　　 )

(A)y₂ >y₃ >y₁(B)y₂ >y₁ >y₃

(C)y₃ >y₁ >y₂ (D)y₃ >y₂ >y₁

1. 反比例函数的解析式与它的图象上的点

例26(1)(沈阳市2007)经过(2，-3)的双曲线是　　　　　　　　 (　　 )

　 (A)y = －　　　(B)y = 　　　　(C)y = 　　　　(D)y = －

(2)如果双曲线y=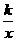经过点(2，-3)，那么此双曲线也经过点　　 (　　　 )

(A)(-3，-2)　 　(B)(-3，2) 　(C)(2，3)　　 (D)(-2，-3)

例27 (1)(安徽省2007年) 近视眼镜的度数 y(度)与镜片焦距 x(米)成反比例. 已知400度近视眼镜镜片的焦距为0.25米，则眼镜度数 y 与镜片焦距 x 之间的函数关系式是　　　　 . (优选y = )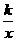

(2) 已知 y = ( 2 - m )x ^{m - 4}是反比例函数，则 m = 　　　, 此函数图象在

第　　　 象限.　　 (优选y = kx ^{- 1}　 )

(3)(北京市海淀区2007年)已知反比例函数 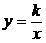　的图象经过

点(1，2)，则函数 y = - kx 可确定为(　 ).

(A)y = - 2x 　(B) y = 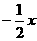　(C) 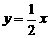　(D)y = 2x

　　　 ( 优选k = xy )

2.　　　 二次函数中的数形结合[用数形结合思想]

例37(1) 抛物线 y = - 3x² + 5x - 4开口　　　 　,　

y = 4x² – 6x + 5 开口　　　　 .

(2)已知： 二次函数 y = ( m – 3 ) x² + 2mx + m + 2，其中m 为常数，且满足-2 < m < 3，此抛物线的开口　　 ，与 x 轴　　　 交点(填有、无)，与 y 轴的交点在x 轴　　　　 (填上方、下方).

　 　(3) 如果二次函数y = 2x² + ( 2a – b )x + b，当且仅当

　1 < x < 2 时，y < 0，那么 a、b 的值是　　　　　 .

(4)(天津市2007)已知二次函数y=ax²+bx+c，且a＜0，a-b+c＞0，则一定有　 (　　　 )

(A)b² - 4ac＞0　　　 (B)b² - 4ac=0　　 (C)b² - 4ac＜0　 (D)b² - 4ac≤0

例38 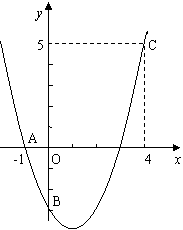(沈阳市2007)如图，二次函数y=ax²+bx+c的图象经过A、B、C三点.

1)观察图象写出A、B、C三点的坐标，并求出此二次函数的解析式；

2)求出此抛物线的顶点坐标和对称轴。

例39 (1)(贵阳市课改实验区2007)已知抛物线y=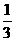(x - 4)² - 3的部分图像(如图) 图像再次与x轴相交时的坐标是　　　　　　　　　　　　　　　　　　　 　(　　 )

(A)　 (5，0)　　　 (B)　 (6，0)　　　　 (C)　 (7，0)　　　　 (D)　 (8，0)

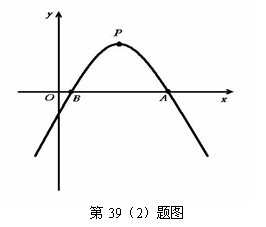
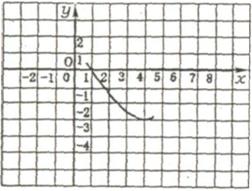
(2) (昆明市2007) 如图，已知二次函数y=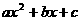 (a≠0)的图象的顶点P的横坐标是4，图象交x轴于点A(m，0)和点B，且m>4，那么AB的长是　　 (　　 )

　　 (A)4+m　 　　　(B)m　 　　　(C)2m一8　 　　　(D)8-2m

1.　　　 二次函数解析式与它图象上的点[用方程思想]

例33(1)抛物线 y = 2x² + bx – 5 过点A ( - 2, 9 )，则关于“b”的方程为　　　　　　 ，此抛物线的解析式为　　　　　　 .

(2)(安徽省2007年)已知函数 y = x² + bx – 1 的图象经过点(3，2).

　1)求这个函数的解析式；

2)画出它的图象，并指出图象的顶点坐标；

(3)抛物线 y = 2x² - 3x – 5 过点A ( n, 9 )，则关于“n”的方程为　　　　　　 ，解得 n = 　　.

(4)抛物线 y = 2x² + bx – 5 过点A ( - 2, y_A )，则 y_A = 　　　　　

(5) 二次函数 y = ax² + bx+ c的图象的顶点A 的坐标为 ( 1, - 3 )，且经过点 B ( -1, 5 )，则设 y = 　　　　　, 得方程为　 　　　　，解得　　　　 ，此函数解析式为 　　　　　　　. (优选顶点式)

(6)二次函数 y = ax² + bx + c的图象与 x 轴交于点A ( - 3, 0 )，对称轴x = -1，顶点C到x轴的距离为2，则设 y = 　　　　　　　, 得方程为　　　　　　 ，解得　　　　　　 ，此函数解析式为 　　　　　　　　　　.　 (优选顶点式)

例34(1) y = - 2x² + 5x – 3 与 y轴的交点的坐标为　 　　　，

(2) y = 2x² – 5x + c 与 y 轴的交点为( 0，3 )，则有c = 　　　　.

(3) y = - 2x² + 5x – 3 与x 轴的交点坐标为　　　　 　、　　　　 .

(4)(安徽省2007年)已知函数 y = x² + bx – 1 的图象经过点(3，2).　

1)求这个函数的解析式；

2)画出它的图象，并指出图象的顶点坐标；

例35　 (1)(常州市2007年)抛物线y = x² - 6x + c 的顶点在 x轴上，则 c 的值是(　 ).

(A) 9　　 (B) 3　　 (C) - 9　　 (D) 0

( 顶点在 x轴上、抛物线与轴相切、抛物线与轴有且仅有一个交点

←　　 →　　　 △ = b² – 4ac = 0)

(2)抛物线 y = - x² + 4x + n - 2 的顶点 P 在 x 轴上，求此抛物线与两坐标轴的交点的坐标.

例36(1)　 抛物线y = - 2 ( x – 3 )² – 7 对称轴 x = 　　　,

顶点坐标为　　　　　 ；

(2)　 抛物线 y = 2x² + 12x – 25 化为　　　　　　　　 ,

对称轴 x = 　　　　　, 顶点坐标为　　　　　　 .

(3)(河北省2007)若将二次函数y=x²－2x + 3配方为y =(x－h)² + k的形式，则y=　　　　　

(4)(贵州市课改实验区2007)抛物线y= - 4(x+2)²+5的对称轴是　　　　　 。

4. 相关的综合题

例32 (1)(辽宁省2007年)已知一次函数 y = kx + b的图象经过第一、二、四象限，则反比例函数 y = 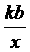的图象是(　 ).

(A) 第一、二象限　　　　　 (B) 第三、四象限

　(C) 第一、三象限　　　　　 (D) 第二、四象限

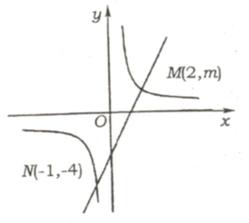
(2)(贵阳市课改实验区2007)如图，一次函数y = ax + b的图像与反比例函数y = 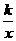的图象交于M、N两点

　　　　 1)求反比例函数和一次函数的解析式；

　2)根据图象写出使反比例函数的值大于一次函数的值的x的取值范围。

(3)(镇江市2007)已知一次函数y = kx + k的图象与反比例函数y = 的图象交于点P(4，n)。

1)求n的值。　　 2)求一次函数的解析式。

二次函数

3. 反比例函数的应用

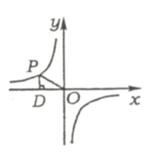例31(南昌市2007)如图，点P是反比例函数y = 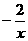上的一点，PD⊥x轴于点D，则△POD的面积为_______.