
题目列表(包括答案和解析)
(一)对直角坐标系的理解[数形结合]
[知识要点]
1. 特殊位置的点的坐标特点
各象限内的点, 坐标轴上的点 例1,例2,例3,例4
[点所在区域决定点坐标的正、负、零, 点到轴的距离决定点坐标的绝对值]
公式: 点到 x 轴的距离 = | y |
点到 y 轴的距离 = | x |
(垂线段的长) = (点坐标的绝对值)
 几何(线段) 函数(坐标)
几何(线段) 函数(坐标)
[转化为线段长用几何知识;转化为点的坐标用函数知识] 例25
象限角平分线上的点[利用坐标间的数量关系构造方程] 例5,例7(2)
 第1、3象限角平分线上的点( x、y ) x = y
第1、3象限角平分线上的点( x、y ) x = y
 第2、4象限角平分线上的点( x、y ) x = - y
第2、4象限角平分线上的点( x、y ) x = - y
2. 两个具有特殊位置的点的坐标间的数量关系 例6
(1)对称性 (2)平行
[利用坐标间的数量关系构造方程]
[基本题型,基本方法]
1. 已知点的坐标 ★ 会求点到坐标轴的距离,
会求同一坐标轴上两点间的距离.
会求两坐标轴上两点间的距离, 会求点到原点的距离,会求仅有一点在坐标轴上的两点间的距离 (用勾股定理)
★ 由已知点的坐标求有关对称点的坐标 例6
★ 求图形变换后点的坐标,会用点的坐标刻化点的移动. 例10
2. 画点的坐标:(略)
3. 求点的坐标:
(1)定域定量法: 例7(1)
(2)构造方程法: 例5,例7(2)
(3)图象交点法:
(4) 观察图象法(含估算)
1)观察点的坐标: 例16,例28(2),例38等等
2)观察已知点有关对称点的坐标: 例6
3)观察函数图象与坐标轴交点的坐标:例16(1),例38,例39
4)观察两个函数图象交点的坐标: 例32(2)
5)观察点的坐标,求函数解析式: 例28(2)
6. 解题方法成为重点 多道例题
5. 直线与几何的结合(比例、勾股、面积等等).
例25,例31,例44,例47,例49,例50,例51,例52 等等
4. 应用. 多道例题
3. 直角坐标系 坐标轴的选取,图形变换. 例10
2. 估算 利用函数图象交点求近似值,预测. 例17,例32(2)
例17 新课程标准P36 例11
填表并观察下列两个函数的变化情况:
|
X |
1 |
2 |
3 |
4 |
5 |
… |
|
Y1 = 50 + 2x |
|
|
|
|
|
|
|
Y2 = 5x |
|
|
|
|
|
|
(1) 在同一个直角坐标系中画出上面两个函数的图象,比较它们有什么不同;
(2) 当 x 从1开始增大时,预测哪一个函数的值先到达100.
1. 移动. 例9,例10,例18,例42,例43,例44
[图形的移动转化为点的移动]
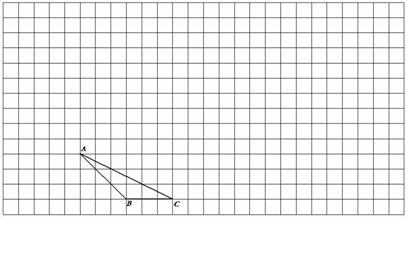
例10 ★★ (海口市课改实验区2007) (1)请在如图所示的方格纸中,将△ABC向上平移3格,再向右平移6格,得△ ,再将△
,再将△ 绕点
绕点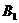 按顺时针方向旋转
按顺时针方向旋转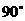 ,得
△
,得
△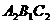 ,最后将△
,最后将△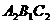 以点
以点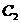 为位似中心放大到2倍,得△
为位似中心放大到2倍,得△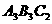 ;
;
(2)请在方格纸的适当位置画上坐标轴(一个小正方形的边长为1个单位长度),在你所建立的直角坐标系中,点C、 、
、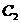 的坐标分别为:点C(_____)、点
的坐标分别为:点C(_____)、点 (_____)、
(_____)、
点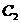 (_____).
(_____).
3. 用待定系数法求函数解析式时,回避三元一次方程组,二元二次方程组,回避一元二次方程根与系数的关系.
提高要求之处:
2. 二次函数交点式不要求.
以《课程标准》为纲,华东师范大学教材、海淀区中考说明为本,海淀教师进修复习指导为依据,抓好三基(基础知识、基本技能、基本能力)、重点内容的落实.
注意《课程标准》与《教学大纲》的相同要求与不同点
降低要求之处:
1. 对《距离》只要求点到坐标轴的距离及同一坐标轴上两点间的距离公式(不能转化为一元二次方程根系关系),不在同一数轴上两点间的距离公式不要求, (可用勾股定理转化为几何问题).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com