
题目列表(包括答案和解析)
1、某商场以每件30元的价格购进一种商品,试销中发现,这种商品每天的销量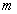 (件)与每件的销售价
(件)与每件的销售价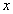 (元)满足一次函数:
(元)满足一次函数: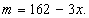
(1)写出商场卖这种商品每天的销售利润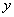 与每件的销售价
与每件的销售价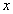 间的函数数关系式.
间的函数数关系式.
(2)如果商场要想每天获得最大的销售利润,每件商品的售价定为多少最合适?最大销售利润为多少?
2. 通过对所得函数关系式进行配方,指出:商场要想每天获得最大的销售利润,每件的销售价定为多少最为合适;最大销售利润为多少?
分析:商场的利润是由每件商品的利润乘每天的销售的数量所决定。
在这个问题中,每件服装的利润为(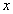
 ),而销售的件数是(
),而销售的件数是(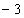 +204),那么就能得到一个
+204),那么就能得到一个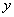 与
与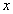 之间的函数关系,这个函数是二次函数.
之间的函数关系,这个函数是二次函数.
要求销售的最大利润,就是要求这个二次函数的最大值.
解:(1)由题意,销售利润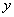 与每件的销售价
与每件的销售价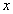 之间的函数关系为
之间的函数关系为
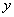 =(
=(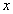 -42)(-3
-42)(-3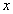 +204),即
+204),即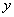 =-3
=-3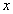 2+
2+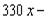 8568
8568
(2)配方,得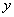 =-3(
=-3(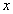 -55)2+507
-55)2+507
∴当每件的销售价为55元时,可取得最大利润,每天最大销售利润为507元.
例2 某跳水运动员进行10米跳台跳水训练时,身体(看成一点)在空中的运动路线是如图所示坐标系下经过原点O的一条抛物线(图中标出的数据为已知条件).
在跳某个规定动作时,正常情况下,该运动员在空中的最高处距水面 米,入水处距池边的距离为4米,运动员在距水面高度为5米以前,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误.
米,入水处距池边的距离为4米,运动员在距水面高度为5米以前,必须完成规定的翻腾动作,并调整好入水姿势,否则就会出现失误.
(1)求这条抛物线的解析式;
(2)在某次试跳中,测得运动员在
空中的运动路线是(1)中的抛物线,
且运动员在空中调整好入水姿势时,距
池边的水平距离为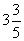 米,问此次跳水会不会失误?
米,问此次跳水会不会失误?
并通过计算说明理由. 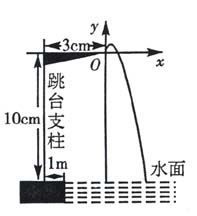
分析:(1)在给出的直角坐标系中,要确定抛物线的解析式,就要确定抛物线上三个点的坐标,如起跳点O(0,0),入水点(2,-10),最高点的纵点标为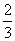 .
.
(2)求出抛物线的解析式后,要判断此次跳水会不会失误,就是要看当该运动员在距池边水平距离为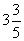 米.,
米.,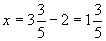 时,该运动员是不是距水面高度为5米.
时,该运动员是不是距水面高度为5米.
解:(1)在给定的直角坐标系下,设最高点为A,入水点为B,抛物线的解析式为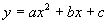 .
.
由题意,知O(0,0),B(2,-10),且顶点A的纵坐标为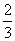 .
.
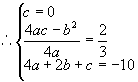

解得 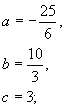 或
或 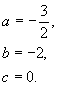
∵抛物线对称轴在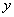 轴右侧,∴
轴右侧,∴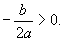
又∵抛物线开口向下,∴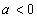 .
.
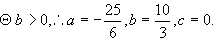
∴抛物线的解析式为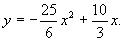
(2)当运动员在空中距池边的水平距离为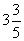 米时,
米时,
 即
即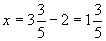 时,
时,
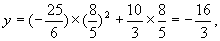
∴此时运动员距水面的高为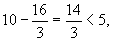
因此,此次跳水会失误.
本节练习题如下:
1.
写出商场卖这种服装每天的销售利润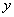 与每件的销售价
与每件的销售价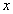 之间的函数关系式(每天的销售利润是指所卖出服装的销售价与购进价的差);
之间的函数关系式(每天的销售利润是指所卖出服装的销售价与购进价的差);
(六) 学会分析方法:
如,函数中的待定系数
已知

 转化点
文字--符号
转化点
文字--符号
的坐标 几何条件
点的坐标 已知的等量关系

 代入函数
用系数的代数
代入函数
用系数的代数
解析式 式表示 …
构造关于系数 ( 如,a、b ) 的方程
 (如, 定c 待a 、b ) 待定的系数越少越好
(如, 定c 待a 、b ) 待定的系数越少越好
定系数 ( 如,a、b、c ) 的值
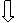
求函数解析式(如,y = ax2 + bx + c ( a ≠ 0 ) )
(五) 构造函数解析式中待定系数的方程的方法:
1. 利用函数的定义(隐含它们最高项的系数 ≠ 0)


 - 一次函数 x的最高指数
= 1
- 一次函数 x的最高指数
= 1
 函数定义 -- 二次函数 x的最高指数
= 2
函数定义 -- 二次函数 x的最高指数
= 2
- 反比例函数 x的指数 = - 1
2. 函数图象上一点坐标满足函数解析式(注意转化点的坐标)
[待定系数法构造关于“系数”方程的主要方法]
3. 利用题目的条件直接构造方程
[用含有待定系数的代数式表示点的坐标]
如,二次函数图象的顶点在x轴上(令 y = 0,Δ ≥ 0 ) 例35
4. 利用几何中公式、定理做为等量关系构造方程 例49
[用含有待定系数的代数式表示线段长]
如,面积公式、勾股定理、相似三角形对应边成比例 等
5. 利用图形中的等量关系构造方程 如, 线段和差 等 例25
(四) 对“点的坐标代入函数解析式”的认识
1. 将已知点的坐标代入函数解析式,构造有关系数的方程; 例33(1)(2)
2. 已知函数解析式及其图象上一点的某坐标,求这点的坐标 例33(3)
[将点的坐标代入函数解析式,构造这点另一坐标的方程]
3. 已知函数解析式及图象上一点(a,b),但a,b未知,求点坐标 例15(7)
[将点的坐标代入函数解析式,构造关于a,b的方程]
[还须一个条件,构造关于a,b的另一个方程]
4. 函数解析式中有待定系数k,点的某坐标a不知道,求函数解析式及点的坐标
[将点的坐标代入函数解析式,构造关于a,k的方程] 例33(4)
5. 用函数解析式中待定系数a、b表示点的坐标,将点的坐标代入另一函数解析式,构造关于a,b的方程
6. 求两个已知函数图象的交点坐标.
[解这两个函数解析式联立的二元一次方程组]
例30(2)(山东省潍坊课改实验区2007)若M(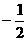 ,y1)、N(
,y1)、N(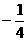 ,y2)、P(
,y2)、P(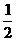 ,y3)三点都在函数y=
,y3)三点都在函数y=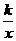 (k < 0)的图像上,则y1
、y2 、y3 的大小关系为 ( )
(k < 0)的图像上,则y1
、y2 、y3 的大小关系为 ( )
 (A)y2 >y3 >y1
(B)y2 >y1 >y3
(A)y2 >y3 >y1
(B)y2 >y1 >y3
(C)y3 >y1 >y2 (D)y3 >y2 >y1
3. 反比例函数的应用 例31
4. 相关的综合题 例32
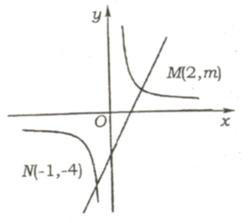
例32 (2)(贵阳市课改实验区)如图,一次函数y= ax + b的图像与反比例函数y=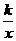 的图象交于M、N两点
的图象交于M、N两点
1)求反比例函数和一次函数的解析式;
2)根据图象写出使反比例函数的值大于一次函数的值的x的取值范围。
二次函数
[基本题型,基本方法]
1. 二次函数解析式与它图象上的点[用方程思想] 例33--例36
二次函数解析式的两种形式(注意隐含条件、优选解析式):
y = ax2 + bx + c ( a ≠ 0 )
y = a(x – h)2 + k ( a ≠ 0 ) (已知对称轴、顶点)
例33 (4) 抛物线 y = 2x2 + bx – 5 过点A ( - 2, yA ),则 yA =
(6) 二次函数 y = ax2 + bx + c的图象与 x 轴交于点A ( - 3, 0 ),
对称轴x = -1,顶点C到x轴的距离为2,则设 y = ,
得方程为 ,解得 ,
此函数解析式为 . (优选顶点式)
2. 二次函数中的数形结合[用数形结合思想](依形判数,由数思形)
看二次函数的图象:
一看与 y 轴交点 ( 0, c ), 定常数项 c. 例38
二看图象的开口方向定 a 的符号: 例37(1)(2)
开口向上 a > 0
开口向下 a < 0
三看抛物线与 x 轴的相对位置: 例37(4) 例41
抛物线与 x 轴有两个交点,⊿ > 0;
抛物线与 x 轴有一个交点,⊿ = 0;
抛物线与 x 轴无交点, ⊿ < 0.
四看抛物线对称轴与 y 轴的相对位置: 例40(1)
对称轴在 y 轴的左侧,a 、b 同号:
对称轴在 y 轴的右侧,a 、b 异号.
五看图象的走向定函数的增减性:(以对称轴为界)
左低右高 y 随 x 增大而增大,
左高右低 y 随 x 增大而减小
六看部分图象对应的取值范围: 例37(3)
(图象端点向 x 轴引垂线,由垂足对应的数看 x 的取值范围)
(图象端点向 y 轴引垂线,由垂足对应的数看 y 的取值范围)
 例38(沈阳市2007)如图,二次函数y=ax2+bx+c的图象经过A、B、C三点.
例38(沈阳市2007)如图,二次函数y=ax2+bx+c的图象经过A、B、C三点.
(1)观察图象写出A、B、C三点的坐标,并求出此二次函数的解析式;
(2)求出此抛物线的顶点坐标和对称轴。
画二次函数图象 (略)
3.图形的移动(翻转,平移,旋转) 例42--例44
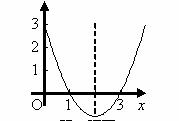
例42(1)(山东省潍坊课改实验区2007)抛物线y=ax2+bx+c如图所示,则它关
于y轴对称的抛物线的解析式为 。
4. 二次函数的应用
例45,例46
二次函数的应用
例45,例46
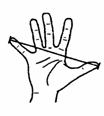
例45 (吉林省2007)如图,大拇指与小拇指尽量张开时,两指尖的距离称为指距.某项研究表明,一般情况下人的身高h是指距d的一次函数.下表是测得的指距与身高的一组数据:
|
指距d(cm) |
20 |
21 |
22 |
23 |
|
身高h(cm) |
160 |
169 |
178 |
187 |
(1) 求出h与d之间的函数关系式(不要求写出自变量d的取值范围):
(2) 某人身高为196cm,一般情况下他的指距应是多少?
5. 相关的综合题 例47--例52
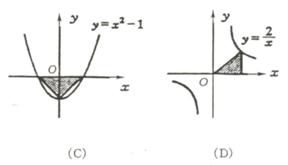
例51下列图中阴影部分的面积与算式|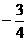 |+(
|+(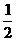 )2
+ 2-1的结果相同的是 ( )
)2
+ 2-1的结果相同的是 ( )
二看图象的位置定函数的增减性:
(三)对三类函数的理解(数形结合)
[知识要点]
|
函数 |
一次函数 |
反比例函数 |
二次函数 |
|
|
解析式 |
y = kx + b (k ≠o) |
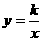 (k ≠o) |
y = ax2
+ bx+c ( a ≠ 0 ) |
|
|
结构 |
结构  形状 形状 |
结构  直线 直线 |
结构  双曲线 双曲线 |
结构  抛物线 抛物线 |
 形状 加条件 结构 形状 加条件 结构 |
不平行于坐标轴的直线
 结构 结构 |
加条件 结构 结构 |
对称轴平行y轴  结构 结构 |
|
 系数 |
定 向 |
 k 定向 k 定向 |
 k 定位置 k 定位置 |
 a符号 开口方向 a符号 开口方向|a| 开口大小 |
|
定 轴 |
-- |
-- |
ab符号  对称轴位置 |
|
|
定 点 (1)与y 轴的交点(交点恰在 y 轴上) (2)抛物线 的顶点 |
b 定点  (0,
b) (0,
b)常数项= 与y轴交点纵坐标 (常数项1 = 常数项2) |
-- |
c
定点 (0, c) (0, c)常数项= 与y轴交点纵坐标 ( 常数项1 = 常数项2 ) |
|
a、b、c
 定点 定点(- 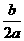 , ,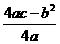 ) ) |
||||
|
定增减性 |
k > 0,y 随 x 增大而增大 k < 0,y 随 x 增大而减小 |
k > 0,y 随 x 增大而减小 k < 0,y 随 x 增大而增大 |
略 |
|
 令y = 0的根x 令y = 0的根x |
定 点 与x 轴的交点 与x 轴的交点 |
令y = 0的根x 定点 定点(x ,0) |
-- |
令y = 0的两根x1,x2 定点 (x1,0),(x2,0) |
一次函数
[基本题型,基本方法]
1. 一次函数的解析式与它图象上的点[用方程思想]
1)求函数解析式 例15(1)(3)(4)(6)
[将点的坐标代入解析式,是构造关于“系数”方程的主要方法]
[转化点的坐标是求函数解析式的重要方法]
求函数解析式的步骤:
一设 (优选函数解析式,尽量用概念定系数,使待定的系数越少越好)
二构 (将点的坐标代入解析式,构造待定系数的方程或方程组,)
(用已知等量关系或几何条件,构造待定系数的方程或方程组)
三解 (解方程或方程组)
四回代(将解出来的系数代入所设的函数解析式)
例15(3) 若一次函数图象过A (2, -1)和B两点,其中点B是另一条直线y =﹣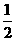 x + 3与y 轴的交点,求这个一次函数的解析式. (定b待k)
x + 3与y 轴的交点,求这个一次函数的解析式. (定b待k)
2)求点的坐标 例15(2)(4)(5)(6)(7)
例15(7) 已知 y = 3x – 2 的图象经过点( a,b ),且 a + b = 6,求a、b的值.
2. 一次函数中的数形结合[用数形结合的思想](依形判数,由数思形)
看一次函数的图象
一看与 y 轴交点 ( 0, b ), 定常数项 b。 例16(1)
二看图象的走向定 k的符号:左低右高 k > 0
左高右低 k < 0 同步练习册 八册下 P17.3
三看图象的走向定函数的增减性: 例16(2)
左低右高 y 随 x 增大而增大,
左高右低 y 随 x 增大而减小
四看图象所在象限定k, b 符号:(略) 同步练习册 八册下 P17.1(2)
画一次函数的图象
例17 新课程标准P36 例11
填表并观察下列两个函数的变化情况:
|
x |
1 |
2 |
3 |
4 |
5 |
… |
|
Y1 = 50 + 2x |
|
|
|
|
|
|
|
Y2 = 5x |
|
|
|
|
|
|
(3) 在同一个直角坐标系中画出上面两个函数的图象,比较它们有什么不同;
(4) 当 x 从1开始增大时,预测哪一个函数的值先到达100.
3.图形的移动(翻转,平移,旋转)
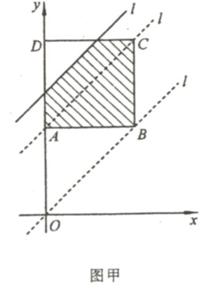
例19 (河南省2007)如图甲,边长为2的正方形ABCD中,顶点A的坐标是(0,2).一次函数y = x + t的图像l随t的不同取值变化时,位于l的右下方由l和正方形的边围成的图像面积为S(阴影部分)
(1) 当t取何值时,S=3
(2) 在平面直角坐标系下(如图乙),画出S与t的图像。
4. 与一次函数有关的实际问题 例20--例24
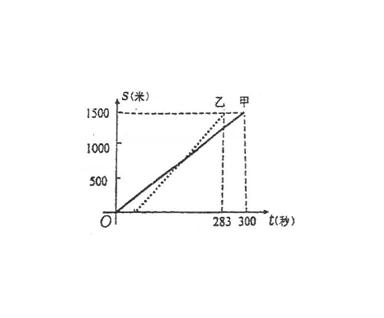
例21 甲、乙两人在一次赛跑中,路程s与时间t的关系如图所示(实线为甲的路程与时间的关系图像,虚线为乙),小王根据图像得到如下四个信息,其中错误的是: ( )
(A) 这是一次1500米的赛跑
(B) 甲、乙两人中先到达终点的是乙
(C) 甲、乙同时起跑
(D) 甲在这次赛跑中的速度为5m/s
反比例函数
[基本题型,基本方法]
1. 反比例函数的解析式与它的图象上的点 例26,例27
例27 (1)(安徽省2007年) 近视眼镜的度数 y(度)与镜片焦距 x(米)成反比例. 已知400度近视眼镜镜片的焦距为0.25米,则眼镜度数 y 与镜片焦距 x 之间的函数关系式是
. (优选y = 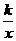 )
)
(2) 已知 y = ( 2 - m )x m - 4是反比例函数,则 m = , 此函数图象在
第 象限. (优选y = kx - 1 )
(3)(北京市海淀区2007年)已知反比例函数 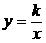 的图象经过
的图象经过
点(1,2),则函数 y = - kx 可确定为( ). ( 优选k = xy )
(A)y = - 2x
(B)
y = 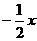 (C)
(C)
 (D)y = 2x
(D)y = 2x
2. 反比例函数中的数形结合(依形判数、由数思形)
看反比例函数图象: 例28--例30
一看图象的位置定 k的符号:
(二)对函数有关概念的理解
[知识要点]
1. 函数定义 2. 函数的图象
[基本题型,基本方法]
1. 函数自变量取值范围
(1)解析式(使解析式有意义) 例11,
(2)图象(图象端点向 x 轴引垂线,由垂足对应的数看 x 的取值范围)例16(1)
★★(3)列表(表中自变量取值)
★★(4)应用(使实际问题有意义)
2. 函数值(实质是求代数式的值): 例12(1)
3. 已知函数值,求自变量取值(实质是解方程): 例12(2)
4. 会画函数图象: 例17
会画直角坐标系(三要素:方向、原点、单位长度)
会画函数图象:
一列表(不能取到的值加括号) 二描点(注意实心点与空心点)
三连线 (注意直线、射线、线段的区别;曲线、曲线段的区别)
四标解析式 (含自变量取值范围)
5. 会求函数图象上的特殊点的坐标:(并到三类函数)
(1)求与 y 轴的交点坐标, ( 0, c ) (看出来的)
(2)求与 x 轴的交点坐标, (算出来的)
1) ( x1,0 ),( x2,0 ) 令 y = 0 解方程解出来的,(Δ ≥ 0)
2) 已知( x1,0 )及对称轴,由对称性得( x2,0 ) (推出来的)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com