25、(12分) 某水果批发商销售每箱进价为40元的苹果，物价部门规定每箱售价不得高于55元，市场调查发现，若每箱以50元的价格销售，平均每天销售90箱，价格每提高1元，平均每天少销售3箱。

(1)求平均每天销售量y(箱)与销售价x(元/箱)之间的函数关系式。(4分)

(2)求该批发商平均每天的销售利润w(元)与销售价x(元/箱)之间的函数关系式(4分)。

(3)当每箱苹果的销售价为多少元时，可以获利最大利润？最大利润是多少？(4分)

24、(8分)如图，点A、B、D、E在⊙O上，弦AE、BD的延长线相交于点C．若AB是⊙O的直径，D是BC的中点．

(1)试判断AB、AC之间的大小关系，并给出证明; (6分)

(2)在上述题设条件下，ΔABC还需满足什么条件，

点E才一定是AC的中点？(直接写出结论)(2分)

第24题

23、(10分)天水市某蔬菜基地有120吨新鲜蔬菜，计划用A，B两种货运车运往外地销售，已知A种车能装载5吨，B种车能装载6吨．

(1)若有A，B两种车共22辆，在满载情况下，能将这些蔬菜全部运完，那么A，B两种车各有多少辆？(5分)

(2)若A种车每辆每趟运费为1500元，B种车每辆每趟运费为1700元，要在车辆满载、且总运费不超过34500元的情况下，将蔬菜全部运完．应怎样选择最佳配车方案？(5分)

22．为迎接2008北京奥运会，某校举行班级乒乓球对抗赛，每个班级选派1对男女混合双打选手参赛，

小明、小亮两名男生准备在小敏、小颖、小丽三名女生中各自随机选择一名组成一对参赛．

(1)列出所有可能的配对结果；

(2)如果小明与小丽、小亮与小敏是最佳组合，那么组成最佳组合的概率是多少？

21．(本小题满分12分)如图，在△ABC中，∠ACB＝90°，BC的垂直平分线DE交BC于D，交AB于E，F在射线DE上，并且EF＝AC．

(1)求证：AF=CE；(6分)

(2)当∠B的大小满足什么条件时，四边形

ACEF是菱形？请回答并证明你的结论；(6分)

20．(本小题满分10分)求一元二次方程x²-x-1=0. 的两个解,方法一:选择合适的一种方法(公式法、配方法、分解因式法求解)求解。解方程：x²-x-1=0即可。

方法二：利用二次函数图象与坐标轴的交点求解，把方程x²-x-1=0.的解看成是二次函数y=　　　　　　

的图象与x轴交点的横坐标，即x₁，x₂就是方程的解。

方法三：如图，利用两个函数图象的交点求解，(1)把方程x²-x-1=0.的解看成是一个二次函数y=　　　　　　

的图象与一个一次函数y=　　　　　　 　的图象交点的横坐标。(2)画出两个函数的图象，用x₁，x₂　　　　 在x轴上标出方程的解。

18、(本小题满分10分)如图，小明与小华爬山时遇到一条笔直的石阶路，路的一侧设有与坡面AB平行的护栏MN(MN=AB)．小明量得每一级石阶的宽为32cm，高为24cm，爬到山顶后，小华数得石阶一共100级，如果每一级石阶的宽和高都一样，且构成直角，请你帮他们求出坡角∠BAC的大小(精确到度)和护栏MN的长度？

16.(10分)如图18格为8×8的正方形网格,请在所给网格中

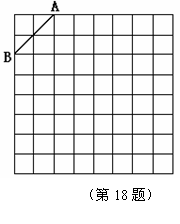按下列要求操作：　　　　

(1)　　　 请在网格中建立平面直角坐标系, 使A点坐

标为(－2，4)，B点坐标为(－4，2)；(3分)

(2) 在第二象限内的格点上画一点C, 使点C与　

线段AB组成一个以AB为底的等腰三角形, 且腰长

是无理数, 则C点坐标是　　　 ， △ABC的周长

是　　　　 (结果保留根号)；(4分)

(3)画出△ABC以点C为旋转中心、旋转180°后的

△A′B′C.(3分)

17(10分)如图，点A是反比例函数的图象与一次函数y＝x+k的图象的一个交点，AC垂直x轴于点C，AD垂直y轴于点D，且矩形OCAD的面积为2．

(1)求这两个函数的解析式；(6分)

(2)求这两个函数图象的另一个交点B的坐标；(4分)

15、观察下列各式：将你猜想到的规律用一个式子来表示：______________________。

14、如图， △ ABC 中，∠B＝ 90 º ，∠C＝ 30 º　 , AB＝1 ，

将 △ ABC 绕顶点 A 旋转 180⁰ ，点 C落在C′处，则 CC′

的长为