
题目列表(包括答案和解析)
4.把二次函数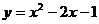 配方成顶点式为( )
配方成顶点式为( )
A.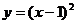 B.
B. 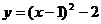
C.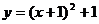 D.
D.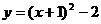
3.抛物线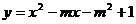 的图象过原点,则
的图象过原点,则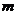 为( )
为( )
A.0 B.1 C.-1 D.±1
2.二次函数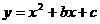 的图象上有两点(3,-8)和(-5,-8),则此拋物线的对称轴是( )
的图象上有两点(3,-8)和(-5,-8),则此拋物线的对称轴是( )
A. =4 B.
=4 B.  =3 C.
=3 C.  =-5 D.
=-5 D.  =-1。
=-1。
1.与抛物线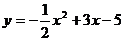 的形状大小开口方向相同,只有位置不同的抛物线是( )
的形状大小开口方向相同,只有位置不同的抛物线是( )
A.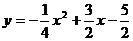 B.
B.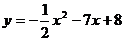
C.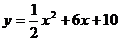 D.
D.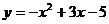
25、解:如图所示,连接CD,∵直线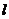 为⊙C的切线,∴CD⊥AD。
为⊙C的切线,∴CD⊥AD。
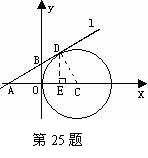 ∵C点坐标为(1,0),∴OC=1,即⊙C的半径为1,∴CD=OC=1。
∵C点坐标为(1,0),∴OC=1,即⊙C的半径为1,∴CD=OC=1。
又∵点A的坐标为(-1,0),∴AC=2,∴∠CAD=30°。
作DE⊥AC于E点,则∠CDE=∠CAD=30°,∴CE=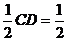 ,
,
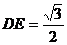 ,∴OE=OC-CE=
,∴OE=OC-CE=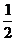 ,∴点D的坐标为(
,∴点D的坐标为(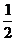 ,
,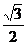 )。
)。
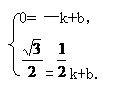 设直线
设直线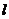 的函数解析式为
的函数解析式为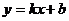 ,则
解得k=
,则
解得k=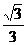 ,b=
,b=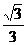 ,
,
∴直线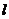 的函数解析式为y=
的函数解析式为y=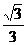 x+
x+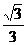 .
.
24、解:(1)不同类型的正确结论有:
①BC=CE ;②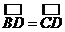 = ③∠BED=90°④∠BOD=∠A;⑤AC∥OD,⑥AC⊥BC;
= ③∠BED=90°④∠BOD=∠A;⑤AC∥OD,⑥AC⊥BC;
⑦OE2+BE2=OB2;⑧S△ABC=BC·OE;⑨△BOD是等腰三角形,⑩△BOE∽△BAC;等
(2)∵OD⊥BC,
∴BE=CE=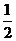 BC=4.
BC=4.
设⊙O的半径为R,则OE=OD-DE=R-2.
在Rt△OEB中,由勾股定理得 OE2+BE2=OB2,即(R-2)2+42=R2.
解得R=5.∴⊙O的半径为5.
25、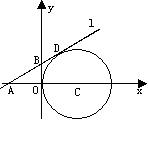 如图,在平面直角坐标系中,⊙C与y轴相切,且C点坐标为(1,0),直线
如图,在平面直角坐标系中,⊙C与y轴相切,且C点坐标为(1,0),直线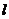 过点A(-1,0),与⊙C相切于点D,求直线
过点A(-1,0),与⊙C相切于点D,求直线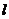 的解析式。
的解析式。
24、 、如图,AB是⊙O的直径,BC是弦,OD⊥BC于E,交
、如图,AB是⊙O的直径,BC是弦,OD⊥BC于E,交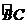 于D.
于D.
(1)请写出五个不同类型的正确结论;
(2)若BC=8,ED=2,求⊙O的半径.
23、圆锥的底面半径为3cm,侧面展开图是圆心角为120º的扇形,求圆锥的侧面积。
22、如图,AB是⊙O的直径,直线PQ过⊙O上的点C,PQ是⊙O的切线。
 求证:∠BCP=∠A
求证:∠BCP=∠A
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com