
题目列表(包括答案和解析)
9.一组数据1,-1,0,-1,1的方差和标准差分别是( )
A.0,0 B.0.8,0.64 C.1,1 D.0.8,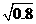
8.某班一次数学测验,其成绩统计如下表:
|
分数 |
50 |
60 |
70 |
80 |
90 |
100 |
|
人数 |
1 |
6 |
12 |
11 |
15 |
5 |
则这个班此次测验的众数为( )
A.90分 B.15 C.100分 D.50分
7.已知一组数据x1,x2,x3,x4,x5的平均数是2,方差为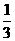 ,那么另一组数据3x1-2,3x2-2,3x3-2,3x4-2,3x5-2的平均数和方差分别是( )
,那么另一组数据3x1-2,3x2-2,3x3-2,3x4-2,3x5-2的平均数和方差分别是( )
A.2,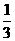 B.2,1 C.4,
B.2,1 C.4,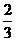 D.4,3
D.4,3
6.甲、乙两个样本的方差分别是s甲2=6.06,s乙2=14.31,由此可反映出( )
A.样本甲的波动比样本乙的波动大;
B.样本甲的波动比样本乙的波动小;
C.样本甲的波动与样本乙的波动大小一样;
D.样本甲和样本乙的波动大小关系不确定
5.某校把学生的笔试、实践能力、成长记录三项成绩分别按50%、20%、30%的比例计入学期总评成绩,90分以上为优秀,甲、乙、丙三人的各项成绩(单位:分)如下表,学期总评成绩优秀的是( )
|
|
笔试 |
实践能力 |
成长记录 |
|
甲 |
90 |
83 |
95 |
|
乙 |
88 |
90 |
95 |
|
丙 |
90 |
88 |
90 |
A.甲 B.乙、丙 C.甲、乙 D.甲、丙
4.一次抽奖活动中,印发的奖券有10 000张,其中特等奖2张,一等奖20张,二等奖98张,三等奖200张,鼓励奖680张,那么第一位抽奖者(仅买一张奖券)中奖的概率为( )
A.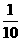 B.
B.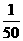 C.
C.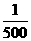 D.
D.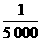
3.下列事件为必然事件的是( )
A.买一张电影票,座位号是偶数; B.抛掷一枚普通的正方体骰子1点朝上
C.百米短跑比赛,一定产生第一名; D.明天会下雨
2.检测1 000名学生的身高,从中抽出50名学生测量,在这个问题中,50名学生的身高是( )
A.个体 B.总体 C.样本容量 D.总体的样本
1.一组数据5,5,6,x,7,7,8,已知这组数据的平均数是6,则这组数据的中位数是( )
A.7 B.6 C.5.5 D.5
(二)不等式与不等式组 2不等式
3不等式(组)
1、几个概念:不等式(组)、不等式(组)的解集、解不等式(组)
2、不等式:
(1)怎样列不等式:
1.掌握表示不等关系的记号
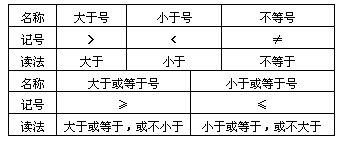
2.掌握有关概念的含义,并能翻译成式子.
(1)和、差、积、商、幂、倍、分等运算.
(2)“至少”、“最多”、“不超过”、“不少于”等词语.
例题:用不等式表示:
①a为非负数,a为正数,a不是正数
解:
②

(2)8与y的2倍的和是正数;
(3)x与5的和不小于0;
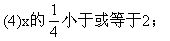
(5)x的4倍大于x的3倍与7的差;
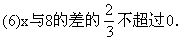
解:
(2)不等式的三个基本性质
不等式的性质1:如果a>b,那么a+c>b+c,a-c>b-c
推论:如果a+c>b,那么a>b-c。
不等式的性质2:如果a>b,并且c>0,那么ac>bc。
不等式的性质3:如果a>b,并且c<0,那么ac<bc。
(3) 解不等式的过程,就是要将不等式变形成x>a或x<a的形式
步骤:(与解一元一次方程类似)
去分母、去括号、移项、合并同类项、系数化一
(注:系数化一时,系数为正不等号方向不变;系数为负方向改变)
例题:①解不等式 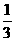 (1-2x)>
(1-2x)>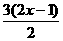
解:
②一本有300页的书,计划10天内读完,前五天因各种原因只读完100页.问从第六天起,每天至少读多少页?
解:
(4)在数轴上表示解集:“大右小左”“”
(5)写出下图所表示的不等式的解集
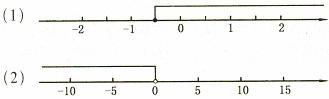
3、不等式组:求解集口诀:同大取大,同小取小,交叉中间,分开两边
例题:①
|
不等式组 |
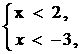 |
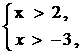 |
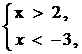 |
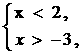 |
|
数轴表示 |
|
|
|
|
|
解集 |
|
|
|
|
②
例题:如果a>b,比较下列各式大小
(1)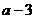
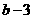 ,(2)
,(2)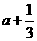
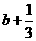 ,(3)
,(3)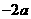
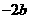
(4)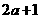
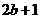 ,(5)
,(5)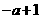
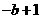
③
[05黄岗]不等式组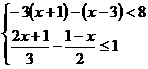 的解集应为( )
的解集应为( )
A、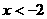 B、
B、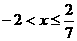 C、
C、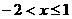 D、
D、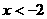 或
或 ≥1
≥1
解
④求不等式组2≤3x-7<8的整数解。
解:
课后练习:
1、下面方程或不等式的解法对不对?
(1)由-x=5,得x=-5;( )
(2)由-x>5,得x>-5;( )
(3)由2x>4,得x<-2;( )
(4)由-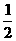 ≤3,得x≥-6。( )
≤3,得x≥-6。( )
2、判断下列不等式的变形是否正确:
(1)由a<b,得ac<bc;( )
(2)由x>y,且m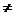 0,得-
0,得-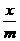 <
<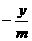 ;( )
;( )
(3)由x>y,得xz2 > yz2;( )
(4)由xz2 > yz2,得x>y;( )
3、把一堆苹果分给几个孩子,如果每人分3个,那么多8个;如果前面每人分5个,那么最后一人得到的苹果不足3个,问有几个孩子?有多少只苹果?
辅导班方程与不等式资料答案:
例题:.解方程:
(1)解:(x=1) (x=1)
(3)[05湘潭] 解: (m=4 )
例题:
①、解下列方程:
解: (1)( x1= 0 x2= 2 ) (2) (x1= 3√5 x2= -3√5 )
(3)(x1=0 x2= 2/3) (4)(x1= - 4 x2= 1)
(5)( t1= - 1 t2= 2 ) (6)(x1= - 4+3√2 x2= - 4-3√2 )
(7)(x1=(3+√15)/2 x2= ( 3-√15)/2 )
(8)(x1= 5 x2= 3/13)
② 填空:(1)x2+6x+( 9 )=(x+ 3 )2;
(2)x2-8x+(16)=(x-4 )2;
(3)x2+ x+(9/16 )=(x+3/4 )2
x+(9/16 )=(x+3/4 )2
例题.①. ( C ) ② B ③.(A)
(4)根与系数的关系:x1+x2= ,x1x2=
,x1x2=
例题:( A )
 例题:[05泸州]解方程组
例题:[05泸州]解方程组 解得: x=5
解得: x=5
y=2
 [05南京]解方程组
[05南京]解方程组  解得: x=2
解得: x=2
y=1
 [05苏州]解方程组:
[05苏州]解方程组: 解得: x=3
解得: x=3
y=1/2
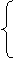 [05遂宁课改]解方程组:
[05遂宁课改]解方程组: 解得 : x=3
解得 : x=3
y=2
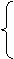 [05宁德]解方程组: 解得: x=3
[05宁德]解方程组: 解得: x=3
y=6
例题:①、解方程: 的解为 ( x= -1 )
的解为 ( x= -1 )
 根为 (x= 2)
根为 (x= 2)
②、[北京市海淀区]( D )
(3)、( A )
例题:①解:设船在静水中速度为x千米/小时
依题意得:80/(x+3)= 60/(x-3) 解得:x=21 答:(略)
②解:设乙车速度为x千米/小时,则甲车的速度为(x+10)千米/小时
依题意得:450/(x+10)=400/x
解得x=80 x+1=90 答:(略)
③解:设原零售价为a元,每次降价率为x
依题意得:a(1-x )²=a/2 解得:x≈0.292 答:(略)
④[05绵阳]解:A=6/5 B= -4/5
⑤解:A
⑥解:三个连续奇数依次为x-2、x、x+2
依题意得:(x-2)² + x² +(x+2)² =371 解得:x=±11
当x=11时,三个数为9、11、13;
当x= -11时,三个数为 -13、-11、-9 答(略)
⑦解:设小正方形的边长为x cm依题意:(60-2x)(40-2x)=800 解得x1=40 (不合题意舍去)
x2=10 答(略)
例题:用不等式表示:①a为非负数,a为正数,a不是正数
解: a≥0 a﹥0 a≤0
② 解:(1)2x/3 -5<1 (2)8+2y>0 (3)x+5≥0
(4)x/4 ≤2 (5)4x>3x-7 (6)2(x-8)/ 3 ≤ 0
例题:①解不等式 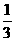 (1-2x)>
(1-2x)>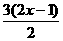
解得:x<1/2
②解:设每天至少读x页
依题意(10-5)x + 100 ≥ 300 解得x≥40 答(略)
(6)写出下图所表示的不等式的解集
 x≥ -1/2
x≥ -1/2
x<0
例题:① ②
例题:如果a>b,比较下列各式大小
(1)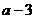 >
>
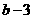 ,(2)
,(2)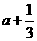 >
> 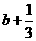 ,(3)
,(3)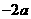 <
<
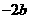
(4)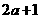 >
> 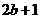 ,(5)
,(5)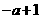 <
<
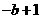
③[05黄岗]( C )
④求不等式组2≤3x-7<8的整数解。解得:3≤x<5
课后练习:
1、下面方程或不等式的解法对不对?
(5)由-x=5,得x=-5;( 对 )
(6)由-x>5,得x>-5;(错 )
(7)由2x>4,得x<-2;( 错 )
(8)由-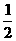 x≤3,得x≥-6。(对 )
x≤3,得x≥-6。(对 )
2、判断下列不等式的变形是否正确:
(5)由a<b,得ac<bc;( 错 )
(6)由x>y,且m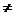 0,得-
0,得-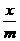 <
<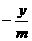 ;( 错 )
;( 错 )
(7)由x>y,得xz2 > yz2;( 错 )
(8)由xz2 > yz2,得x>y;(对 )
3、把一堆苹果分给几个孩子,如果每人分3个,那么多8个;如果前面每人分5个,那么最后一人得到的苹果不足3个,问有几个孩子?有多少只苹果?
解:设有x个孩,依题意:3x+8 - 5(x-1)<3 解得5<x≤6.5
X=6 答(略)
本资料由《七彩教育网》 提供!
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com