
题目列表(包括答案和解析)
5.已知一个凸四边形ABCD的四条边长依次是a、b、c、d,且a2+ab-ac-bc=0,b2+bc-bd-cd=0,那么四边形ABCD是( )
A.平行四边形 B.矩形 C.菱形 D.梯形
4.现规定一种运算:a*b=ab+a-b,其中a、b为常数,则2*3+1*4等于( )
A.10 B.6 C.14 D.12
3.用正方形在日历中任意框出的四个数一定能被( )整除
A.3 B.4 C.5 D.6
2.x的5倍与y的差等于( )
A.5x-y B.5(x-y) C.x-5y D.x5-y
1.在x,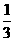 ,
,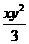 ,
,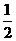 x+
x+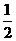 y,xy-2,
y,xy-2,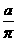 中,单项式有(
)
中,单项式有(
)
A.2个 B.3个 C.4个 D.5个
26、(重庆市2007T28)(10分)已知,在Rt△OAB中,∠OAB=900,∠BOA=300,AB=2。若以O为坐标原点,OA所在直线为 轴,建立如图所示的平面直角坐标系,点B在第一象限内。将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处。
轴,建立如图所示的平面直角坐标系,点B在第一象限内。将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处。
(1)求点C的坐标;
(2)若抛物线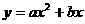 (
(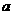 ≠0)经过C、A两点,求此抛物线的解析式;
≠0)经过C、A两点,求此抛物线的解析式;
(3)若抛物线的对称轴与OB交于点D,点P为线段DB上一点,过P作 轴的平行线,交抛物线于点M。问:是否存在这样的点P,使得四边形CDPM为等腰梯形?若存在,请求出此时点P的坐标;若不存在,请说明理由。
轴的平行线,交抛物线于点M。问:是否存在这样的点P,使得四边形CDPM为等腰梯形?若存在,请求出此时点P的坐标;若不存在,请说明理由。
 注:抛物线
注:抛物线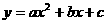 (
(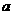 ≠0)的顶点坐标为
≠0)的顶点坐标为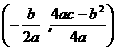 ,对称轴公式为
,对称轴公式为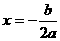
解:(1)过点C作CH⊥ 轴,垂足为H
轴,垂足为H
∵在Rt△OAB中,∠OAB=900,∠BOA=300,AB=2
∴OB=4,OA=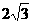
由折叠知,∠COB=300,OC=OA=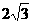
∴∠COH=600,OH= ,CH=3
,CH=3
∴C点坐标为( ,3)
,3)
(2)∵抛物线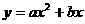 (
(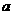 ≠0)经过C(
≠0)经过C( ,3)、A(
,3)、A(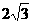 ,0)两点
,0)两点
∴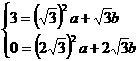 解得:
解得: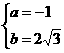
∴此抛物线的解析式为: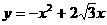
(3)存在。因为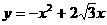 的顶点坐标为(
的顶点坐标为( ,3)即为点C
,3)即为点C
MP⊥ 轴,设垂足为N,PN=
轴,设垂足为N,PN=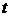 ,因为∠BOA=300,所以ON=
,因为∠BOA=300,所以ON=
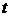
∴P(
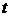 ,
,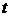 )
)
作PQ⊥CD,垂足为Q,ME⊥CD,垂足为E
把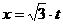 代入
代入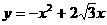 得:
得: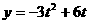
∴ M(
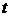 ,
,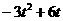 ),E(
),E( ,
,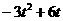 )
)
同理:Q( ,
,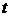 ),D(
),D( ,1)
,1)
要使四边形CDPM为等腰梯形,只需CE=QD
即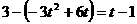 ,解得:
,解得: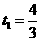 ,
,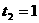 (舍)
(舍)
∴ P点坐标为( ,
, )
)
∴ 存在满足条件的点P,使得四边形CDPM为等腰梯形,此时P点的坐为( ,
, )
)
本资料由《七彩教育网》 提供!
25、(10分)(山东济南课改卷)如图1,已知 中,
中, ,
,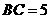 .过点
.过点 作
作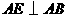 ,且
,且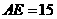 ,连接
,连接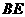 交
交 于点
于点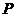 .
.
(1)求 的长;
的长;
(2)以点 为圆心,
为圆心,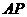 为半径作
为半径作 ,试判断
,试判断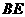 与
与 是否相切,并说明理由;
是否相切,并说明理由;
(3)如图2,过点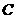 作
作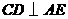 ,垂足为
,垂足为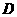 .以点
.以点 为圆心,
为圆心, 为半径作
为半径作 ;以点
;以点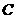 为圆心,
为圆心,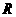 为半径作
为半径作 .若
.若 和
和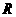 的大小是可变化的,并且在变化过程中保持
的大小是可变化的,并且在变化过程中保持 和
和 相切,且使
相切,且使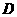 点在
点在 的内部,
的内部, 点在
点在 的外部,求
的外部,求 和
和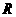 的变化范围.
的变化范围.
[解] (1) 在
在 中,
中,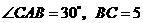 ,
,
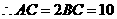 .
.
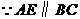 ,
,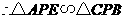 .
.
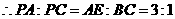 .
.
 ,
,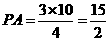 .
.
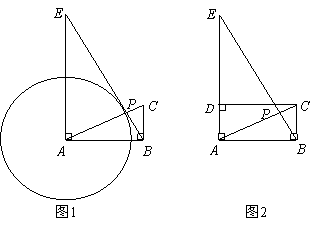
(2)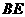 与
与 相切.
相切.
 在
在 中,
中,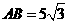 ,
,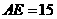 ,
,
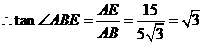 ,
,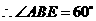 .
.
又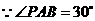 ,
,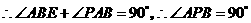 ,
,
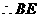 与
与 相切.
相切.
(3)因为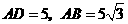 ,所以
,所以 的变化范围为
的变化范围为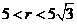 .
.
当 与
与 外切时,
外切时,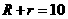 ,所以
,所以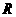 的变化范围为
的变化范围为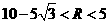 ;
;
当 与
与 内切时,
内切时,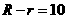 ,所以
,所以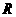 的变化范围为
的变化范围为 .
.
23.(1)设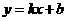 ,由题意得
,由题意得
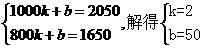
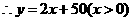 --------------------------------(3分)
--------------------------------(3分)
(2)AD=1250米,B到C的价格为1250元,-----------(6分)
(3)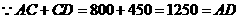
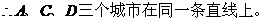 --------------(8分)
--------------(8分)
(4)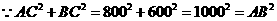
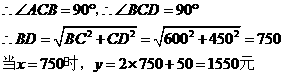
答:从B市直接飞到D市的机票价格应定为1550元。-----------(10分)
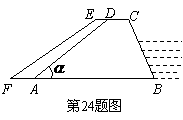
24(08泰州)如图,某堤坝的横截面是梯形 ,背水坡
,背水坡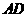 的坡度i(即
的坡度i(即 )为1∶1.2,坝高为5米.现为了提高堤坝的防洪抗洪能力,市防汛指挥部决定加固堤坝,要求坝顶
)为1∶1.2,坝高为5米.现为了提高堤坝的防洪抗洪能力,市防汛指挥部决定加固堤坝,要求坝顶 加宽1米,形成新的背水坡
加宽1米,形成新的背水坡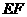 ,其坡度为1∶1.4.已知堤坝总长度为4000米.
,其坡度为1∶1.4.已知堤坝总长度为4000米.
(1)求完成该工程需要多少土方?(4分)
(2)该工程由甲、乙两个工程队同时合作完成,按原计划需要20天.准备开工前接到上级通知,汛期可能提前,要求两个工程队提高工作效率.甲队工作效率提高30%,乙队工作效率提高40%,结果提前5天完成.问这两个工程队原计划每天各完成多少土方?(4分)
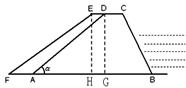
解:(1)作DG⊥AB于G,作EH⊥AB于H.
∵CD∥AB, ∴EH=DG=5米,
∵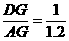 ,∴AG=6米,…………………………………………1分
,∴AG=6米,…………………………………………1分
∵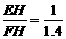 ,∴FH=7米, …………………………………………2分
,∴FH=7米, …………………………………………2分
∴FA=FH+GH-AG=7+1-6=2(米)…………………………………3分
∴SADEF=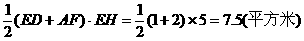 .
.
V=7.5×4000=30000(立方米). ……………………………………4分
(2)设甲队原计划每天完成x立方米土方, 乙队原计划每天完成y立方米土方.
根据题意,得 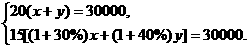 …………………6分
…………………6分
化简,得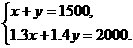 …………………………………………7分
…………………………………………7分
解之,得 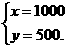 ……………………………………………………………8分
……………………………………………………………8分
答:甲队原计划每天完成1000立方米方土, 乙队原计划每天完成500立方米方土. ……………………………9分
23、(2007重庆一中25) (8分)某航空公司经营A、B、C、D四个城市之间的客运业务. 若机票价格y(元)是两城市间的距离x(千米)的一次函数. 今年“五、一”期间部分机票价格如下表所示:
(1)求该公司机票价格y(元)与距离x(千米)的函数关系式;
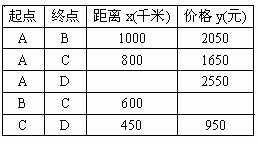 (2)利用(1)中的关系式将表格填完整;
(2)利用(1)中的关系式将表格填完整;
(3)判断A、B、C、D这四个城市中,哪三个
城市在同一条直线上?请说明理由;
(4)若航空公司准备从旅游旺季的7月开始增
开从B市直接飞到D市的旅游专线,且按以上
规律给机票定价,那么机票定价应是多少元?
22。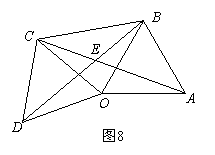 (2008中山市)(本题满分8分)(1)如图7,点O是线段AD的中点,分别以AO和DO为边在线段AD的同侧作等边三角形OAB和等边三角形OCD,连结AC和BD,相交于点E,连结BC.求∠AEB的大小;
(2008中山市)(本题满分8分)(1)如图7,点O是线段AD的中点,分别以AO和DO为边在线段AD的同侧作等边三角形OAB和等边三角形OCD,连结AC和BD,相交于点E,连结BC.求∠AEB的大小;
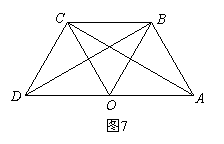
(2)如图8,ΔOAB固定不动,保持ΔOCD的形状和大小不变,将ΔOCD绕着点O旋转(ΔOAB和ΔOCD不能重叠),求∠AEB的大小.
解:(1)如图7.
∵ △BOC和△ABO都是等边三角形,
且点O是线段AD的中点,
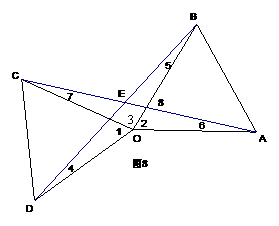 ∴ OD=OC=OB=OA,∠1=∠2=60°,
∴ OD=OC=OB=OA,∠1=∠2=60°,
∴ ∠4=∠5.
又∵∠4+∠5=∠2=60°,
∴ ∠4=30°.
同理,∠6=30°.
∵ ∠AEB=∠4+∠6,
∴ ∠AEB=60°.
(2)如图8.
∵ △BOC和△ABO都是等边三角形,
∴ OD=OC, OB=OA,∠1=∠2=60°,
又∵OD=OA,
∴ OD=OB,OA=OC,
∴ ∠4=∠5,∠6=∠7.
∵ ∠DOB=∠1+∠3,
∠AOC=∠2+∠3,
∴∠DOB=∠AOC.
∵ ∠4+∠5+∠DOB=180°, ∠6+∠7+∠AOC=180°,
∴ 2∠5=2∠6,
∴ ∠5=∠6.
又∵ ∠AEB=∠8-∠5, ∠8=∠2+∠6,
∴ ∠AEB=∠2+∠5-∠5=∠2,
∴ ∠AEB=60°.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com