
题目列表(包括答案和解析)
25.(12分)如图,已知平行四边形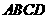 的顶点
的顶点 的坐标是
的坐标是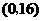 ,
,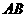 平行于
平行于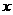 轴,
轴,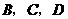 三点在抛物线
三点在抛物线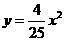 上,
上,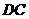 交
交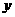 轴于
轴于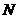 点,一条直线
点,一条直线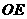 与
与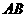 交于
交于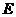 点,与
点,与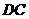 交于
交于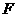 点,如果
点,如果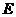 点的横坐标为
点的横坐标为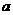 ,四边形
,四边形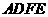 的面积为
的面积为 .
.
(1)求出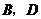 两点的坐标;
两点的坐标;

(2)求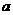 的值;
的值;
(3)作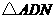 的内切圆⊙P,切点分别为
的内切圆⊙P,切点分别为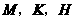 ,求
,求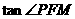 的值.
的值.
24.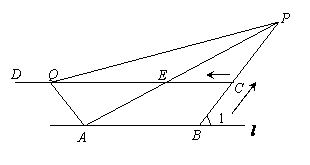 (10分)如图9,A、B是直线
(10分)如图9,A、B是直线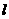 上的两点,AB=4厘米,过
上的两点,AB=4厘米,过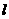 外一点C作CD∥
外一点C作CD∥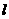 ,射线BC与
,射线BC与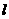 所成的锐角∠1=60°,线段BC=2厘米,动点P、Q分别从B、C同时出发,P以每秒1厘米的速度沿由B向C的方向运动,Q以每秒2厘米的速度沿由C向D的方向运动.设P,Q运动的时间为t(秒),当t>2时,PA交CD于E.
所成的锐角∠1=60°,线段BC=2厘米,动点P、Q分别从B、C同时出发,P以每秒1厘米的速度沿由B向C的方向运动,Q以每秒2厘米的速度沿由C向D的方向运动.设P,Q运动的时间为t(秒),当t>2时,PA交CD于E.
(1) 求△APQ的面积S与t的函数关系式.
(2) QE恰好平分△APQ的面积时,试求QE的长是多少厘米?
图9
23.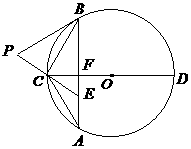 (8分)如图8,已知⊙
(8分)如图8,已知⊙ 的弦
的弦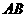 垂直于直径
垂直于直径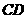 ,垂足为
,垂足为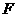 ,连接
,连接 、
、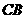 .
.
(1)求证: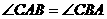 ;
;
(2)在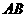 上有一点
上有一点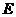 ,延长
,延长 到点
到点 ,连接
,连接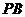 ,
,
若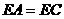 ,
,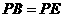 ,求证:
,求证: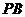 是⊙
是⊙ 的切线.
的切线.
图8
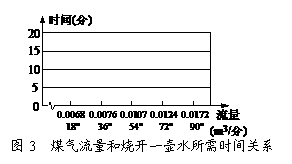 (1).作图:将下面图2中的直方图补充完整;在图3中作出流量与时间的折线图.
(1).作图:将下面图2中的直方图补充完整;在图3中作出流量与时间的折线图.
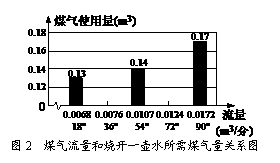

(2).填空:①从图2可以看出,烧开一壶水所耗用的最少煤气量为_______m2,此时旋钮位置在______.
②从图3可以看出,不考虑煤气用量,烧开一壶水所用的最短时间为_______分钟,此时旋钮位置在______.
(3).通过实验,请你对上述结果(用煤气烧水最省时和最省气)作一个简要的说明.
21.(8分) 某县响应“建设环保节约型社会”的号召,决定资助部分付镇修建一批沼气池,使农民用到经济、环保的沼气能源.幸福村共有264户村民,政府补助村里34万元,不足部分由村民集资.修建A型、B型沼气池共20个.两种型号沼气池每个修建费用、可供使用户数、修建用地情况如下表:
|
沼气池 |
修建费用(万元/个) |
可供使用户数(户/个) |
占地面积(m2/个) |
|
A型 |
3 |
20 |
48 |
|
B型 |
2 |
3 |
6 |
政府相关部门批给该村沼气池修建用地708m2.设修建A型沼气池x个,修建两种型号沼气池共需费用y万元.
(1)求y与x之间的函数关系式;
(2)不超过政府批给修建沼气池用地面积,又要使该村每户村民用上沼气的修建方案有几种;
(3)若平均每户村民集资700元,能否满足所需费用最少的修建方案.
20.(8分)一、问题背景
某校九年级(1)班课题学习小组对家庭煤气的使用量做了研究,其实验过程和对数据的处理如下.
仔细观察现在家庭使用的电子打火煤气灶,发现当关着煤气的时候,煤气旋钮(以下简称旋钮)的位置为竖起方向,把这个位置定为0°,煤气开到最大时,位置为90°.(以0°位置作起始边,旋钮和起始边的夹角).在0~90°之间平均分成五等分,代表不同的煤气流量,它们分别是18°,36°,54°,72°,90°,见图1.


|
位置 |
烧开一壶水所需 |
流量 |
|
|
时间(分) |
煤气量(m3) |
m3/分 |
|
|
18° |
19 |
0.13 |
0.0068 |
|
36° |
16 |
0.12 |
0.0076 |
|
54° |
13 |
0.14 |
0.0107 |
|
72° |
12 |
0.15 |
0.0124 |
|
90° |
10 |
0.17 |
0.0172 |
在这些位置上分别以烧开一壶水(3.75升)为标准,记录所需的时间和所用的煤气量.并根据旋钮位置以及烧开一壶水所需时间(用t表示)、所用煤气量(用v表示),计算出不同旋钮位置所代表的煤气流量(用L表示),L=v/t,数据见右表.这样为可以研究煤气流量和烧开一壶水所需时间及用气量之间的关系了.
19.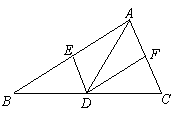 (7分)如图7,已知点D在△ABC的BC边上,DE∥AC交AB于E,DF∥AB交AC于F.
(7分)如图7,已知点D在△ABC的BC边上,DE∥AC交AB于E,DF∥AB交AC于F.
(1)求证:AE=DF;
(2)若AD平分∠BAC,试判断四边形AEDF的形状,并说明理由.
图7
18.(6分)如图6,某小区有一长100m,宽80cm的空地,现将其建成花园广场,设计图案如下,阴影区域为绿化区(四块绿化区是全等矩形),空白区域为活动区,且四周出口一样宽,宽度不小于50m,不大于60m.预计活动区每平方米造价60元,绿化区每平方米造价50元.
(1)设一块绿化区的长边为xm,写出工程总造价y与x的函数关系式(写出x的取值范围);
 (2)如果小区投资46.9万元,问能否完成工程任务,若能,请写出x为整数的所有工程方案;若不能,请说明理由.(参考值:
(2)如果小区投资46.9万元,问能否完成工程任务,若能,请写出x为整数的所有工程方案;若不能,请说明理由.(参考值: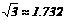 )
)
17.(5分)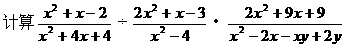
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com