
题目列表(包括答案和解析)
3.二次函数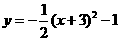 的顶点为[ ]
的顶点为[ ]
A.(3,-1) B.(3,1) C.(-3,1) D.(-3,-1)
2.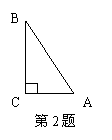 如图,在△ABC中,AC=3,BC=4,∠C=90º,SinB的值是 [ ]
如图,在△ABC中,AC=3,BC=4,∠C=90º,SinB的值是 [ ]
A.
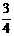 B.
B. 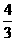 C.
C. 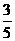 D.
D. 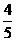
1.一元二次方程x2-2x-3=0的根为 [ ]
A.x1=1,x2=3 B.x1= -1,x2=3 C.x1= -1,x2= -3 D.x1=1,x2= -3
23.如图①,OP是∠MON的平分线,请你利用该图形画一对以OP所在直线为对称轴的全等三角形。请你参考这个作全等三角形的方法,解答下列问题:
(1)如图②,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F。请你判断并写出FE与FD之间的数量关系;
(2)如图③,在△ABC中,如果∠ACB不是直角,而(1)中的其它条件不变,请问,你在(1)中所得结论是否仍然成立?若成立,请证明;若不成立,请说明理由。
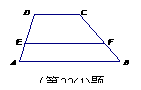
22.(1)如图,在梯形ABCD中,AB∥CD,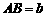 ,
,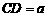 ,E为AD边上的任意一点,EF∥AB,且EF交BC于点F,某学生在研究这一问题时,发现如下事实:
,E为AD边上的任意一点,EF∥AB,且EF交BC于点F,某学生在研究这一问题时,发现如下事实:
 ①当
①当 时,有
时,有 ; ②当
; ②当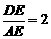 时,有
时,有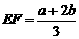 ;
;
③当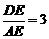 时,有
时,有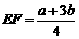 . 当
. 当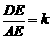 时,参照上述
时,参照上述
研究结论,请你猜想用k表示EF的一般结论,并给出证明;
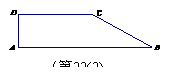 (2)现有一块直角梯形田地
(2)现有一块直角梯形田地 (如图所示),其中AB∥CD,
(如图所示),其中AB∥CD,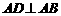 ,
,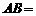 310米,
310米, 170米,
170米,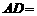 70米.若要将这块地分割成两块,由两农户来承包,要求这两块地均为直角梯形,且它们的面积相等.请你给出具体分割方案.
70米.若要将这块地分割成两块,由两农户来承包,要求这两块地均为直角梯形,且它们的面积相等.请你给出具体分割方案.
21. 如图,⊙O的直径AB=4,∠ABC=30o ,BC=
如图,⊙O的直径AB=4,∠ABC=30o ,BC=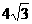 ,D是线段BC的中点。
,D是线段BC的中点。
(1)试判断点D与⊙O的位置关系,并说明理由;
(2)过点D作DE⊥AC,垂足为点E,求证:直线DE是⊙O
的切线。
20. 如图,隧道的截面由圆弧AED和矩形ABCD构成,矩形的长BC为12m,宽AB为3m,隧道的顶端E(圆弧AED的中点)高出道路BC 7m.
如图,隧道的截面由圆弧AED和矩形ABCD构成,矩形的长BC为12m,宽AB为3m,隧道的顶端E(圆弧AED的中点)高出道路BC 7m.
⑴求圆弧AED所在圆的半径;
⑵如果该隧道内设双行道,现有一辆超高货运卡车高6.5m,宽2.3m,问这辆货运卡车能否通过该隧道?
19.我们给出如下定义:若一个四边形的两条对角线相等,则称这个四边形为等对角线四边形。请解答下列问题:
(1)写出你所学过的特殊四边形中是等对角线四边形的两种图形的名称;
(2)探究:当等对角线四边形中两条对角线所夹锐角为60°时,这对60°角所对的两边之和与其中一条对角线的大小关系,并证明你的结论。
18.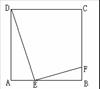 如图,E是正方形ABCD的边AB上的动点, EF⊥DE交BC于点F.
如图,E是正方形ABCD的边AB上的动点, EF⊥DE交BC于点F.
(1)求证: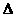 ADE∽
ADE∽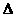 BEF;
BEF;
(2)设正方形的边长为4, AE=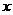 ,BF=
,BF=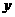 .当
.当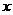 取什么值时,
取什么值时, 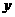 有最大值?并求出这个最大值.
有最大值?并求出这个最大值.
17.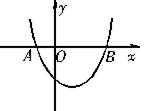 如图,经过点M(-1,2),N(1,-2)的抛物线y=ax2+bx+c与x的交于A、B两点,与y轴交于C点.
(1)求b的值;
(2)若OC2=OA·OB,试求抛物线的解析式;
如图,经过点M(-1,2),N(1,-2)的抛物线y=ax2+bx+c与x的交于A、B两点,与y轴交于C点.
(1)求b的值;
(2)若OC2=OA·OB,试求抛物线的解析式;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com