23．(11分)如图，对称轴为直线x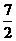＝的抛物线经过点A(6，0)和B(0，4)． (1)求抛物线解析式及顶点坐标；

(2)设点E(x，y)是抛物线上一动点，且位于第四象限，四边形OEAF是以OA为对角线的平行四边形，求四边形OEAF的面积S与x之间的函数关系式，并写出自变量x的取值范围；

(3)①当四边形OEAF的面积为24时，请判断OEAF是否为菱形？

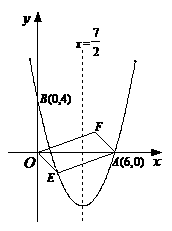②是否存在点E，使四边形OEAF为正方形？若存在，求出点E的坐标；若不存在，请说明理由．

22．(10分)如图，在梯形ABCD中，AB∥CD，∠BCD=90°,且AB=1，BC=2，tan∠ADC=2.

(1)　　 求证：DC=BC;

(2)　　 E是梯形内一点，F是梯形外一点，且∠EDC=∠FBC，DE=BF，试判断△ECF的形状，并证明你的结论；

(3)　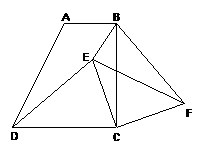　 在(2)的条件下，当BE：CE=1：2，∠BEC=135°时，求sin∠BFE的值.

21．(10分)请你画出一个以BC为底边的等腰ΔABC，使底边上的高AD=BC．(1)求tanB和 sinB的值；

(2)在你画的等腰ΔABC中设底边BC=5米，求腰上的高BE．

20．(9分)如图，已知BC为半圆的直径，O为圆心，D是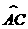的中点，四边形ABCD对角线AC、BD交于点E．

(1)求证：△ABE∽△DBC；

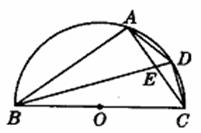(2)已知BC=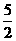，CD=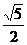，求sin∠AEB的值；

(3)在(2)的条件下，求弦AB的长．

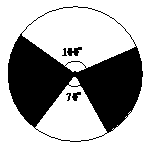
19．(9分)张彬和王华两位同学为得到一张观看足球比赛的入场券，各自设计了一种方案：

张彬：如图，设计了一个可以自由转动的转盘，随意转动转盘，当指针指向阴影区域时，张彬得到了入场券；否则，王华得到入场券；

王华：将三个完全相同的小球分别标上数字1、2、3后，放入一个不透明的袋子中．从中随机取出一个小球，然后放回袋子；混合均匀后，再随机取出一个小球．若两次取出的小球上的数字之和为偶数，王华得到入场券；否则，张彬得到入场券．

请你运用所学的概率知识，分析张彬和王华的设计方案对双方是否公平．

18．(9分)如图，边长为1的正方形OABC的顶点O为坐标原点，点A在x轴的正半轴上，点C在y轴的正半轴上．动点D在线段BC上移动(不与B，C重合)，连接OD，过点D作DE⊥OD，交边AB于点E，连接OE．记CD的长为t．如果记梯形COEB的面积为S，那么是否存在S的最大值？若存在，请求出这个最大值及此时t的值；若不存在，请说明理由。

17．(9分)已知：如图，□ABCD中，E、F分别是AB、CD的中点.

求证：△AFD≌CEB．

16．(8分) 计算：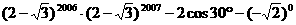

15．如图，把一个矩形纸片OABC放入平面直角坐标系中，使OA、OC分别落在x轴、y轴上，连结OB，将纸片OABC沿OB折叠，使点A落在A’的位置上．若OB=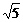，tan∠AOB=2，求点A’的坐标为_______________．

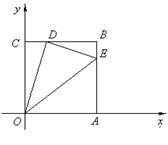
14．如图，四边形OABC为菱形，点B、C在以点O为圆心的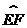上，

若OA=3，∠1=∠2，则扇形OEF的面积为　　　　　　 ．