
题目列表(包括答案和解析)
4. 已知一元二次方程x2-6x+5-k=0的根的判别式 =4,k= .
=4,k= .
3. 圆内接四边形ABCD的内角∠A:∠C=1:3,则∠C= °.
2. 已知二次函数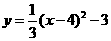 ,它的最小值是 .
,它的最小值是 .
1. 将抛物线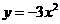 向上平移一个单位后,得到的抛物线解析式是 .
向上平移一个单位后,得到的抛物线解析式是 .
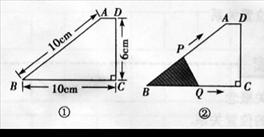
26.(本小题满分12分)如图①,在梯形ABCD中,AB=BC=10 cm,CD=6 cm,∠C=∠D=90°,
如图②,动点P、Q同时以每秒1cm的速度从点B出发,点P沿BA、AD、DC运动到点C停止,点Q沿BC运动到点C停止。
(1)设P、Q同时从点B出发t秒时,△PBQ的面积为S(cm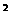 ),求S(cm
),求S(cm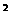 )关于t(秒)的函数关系式;并写出自变量t的取值范围.
)关于t(秒)的函数关系式;并写出自变量t的取值范围.
(2)当t为何值时,△PBQ的面积最大?最大面积是多少?
25.(本小题满分12分)暑假期间,王明到承德雾灵山风景区--景区主峰为燕山最高峰(海拔达1834米),位于承德市兴隆县境内旅游。导游介绍山区气温会随着海拔高度的增加而下降,提醒大家上山要多带一件衣服,王明从旅馆中得到一份残缺的雾灵山地区海拔和气温数据表(温差不超过2℃),数据如下:
|
海拔高度x(米) |
400 |
500 |
600 |
700 |
800 |
…… |
|
气温y(℃) |
29.2 |
28.6 |
28.0 |
27.4 |
26.8 |
…… |
 (1)以海拔高度为x轴,根据上表提供的数据在下列直角坐标系中描点并连线。
(1)以海拔高度为x轴,根据上表提供的数据在下列直角坐标系中描点并连线。
(2)观察(1)中所画出的图像,猜想y与x之间函数关系,求出所猜想的函数关系表达式,并根据表中提供的数据验证你的猜想;
(3)如果气温低于20℃就需要穿外套,请问王明需不需要携带外套上山?
24.(本小题满分10分)如图15,直线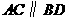 ,连结
,连结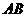 ,直线
,直线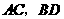 及线段
及线段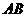 把平面分成①、②、③、④四个部分,规定线上各点不属于任何部分.当动点
把平面分成①、②、③、④四个部分,规定线上各点不属于任何部分.当动点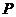 落在某个部分时,连结
落在某个部分时,连结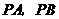 ,构成
,构成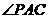 ,
,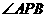 ,
,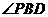 三个角.
三个角.
(1)当动点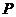 落在第①部分时,求证:
落在第①部分时,求证: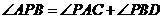 ;
;
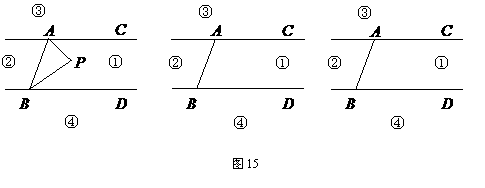
(2)当动点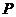 落在第②部分时,
落在第②部分时,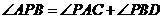 是否成立
是否成立
 (3)当动点
(3)当动点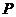 在第③部分时,全面探究
在第③部分时,全面探究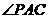 ,
,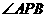 ,
,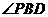 之间的关系,并写出动点
之间的关系,并写出动点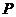 的具体位置和相应的结论.选择其中一种结论加以证明.
的具体位置和相应的结论.选择其中一种结论加以证明.
23.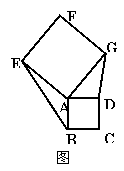
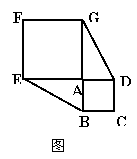
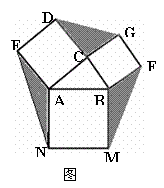 (本小题满分10分)已知正方形ABCD和正方形AEFG有公共顶点A,将正方形AEFG绕点A旋转
(本小题满分10分)已知正方形ABCD和正方形AEFG有公共顶点A,将正方形AEFG绕点A旋转
(1)发现:当E点旋转到DA的延长线上时(如图12-1),△ABE与△ADG的面积关系是:_______.
(2)引申:当正方形AEFG旋转任意一个角度时(如图12-2),△ABE与△ADG的面积关系是:________.并证明你的结论
(3)运用:已知△ABC,AB=5,AC=4,分别以AB、BC、CA为边向外作正方形(如图12-3),则图中阴影部分的面积和的最大值是__________.
22.(本小题满分8分)如图11,抛物线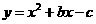 和
和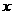 轴交于
轴交于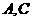 两点,和y轴交于
两点,和y轴交于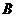 点,抛物线的顶点为
点,抛物线的顶点为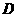 ,OA=OB=3.
,OA=OB=3.
(1)求此抛物线的解析式;
(2)点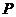 为x轴下方抛物线上的一个点,求使
为x轴下方抛物线上的一个点,求使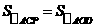 的点
的点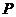 的坐标.
的坐标.

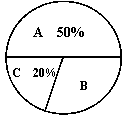
21.(本小题满分10分)自从北京获得2008年夏季奥运会申办权以来,奥运知识在我国不断传播,小刚就本班学生的对奥运知识的了解程度进行了一次调查统计.A:熟悉,B:了解较多,C:一般了解.图10-1和图10-2是他采集数据后,绘制的两幅不完整的统计图,请你根据图中提供的信息解答以下问题:
(1)求该班共有多少名学生
(2)在条形图中,将表示“一般了解”的部分补充完整.
(3)在扇形统计图中,计算出“了解较多”部分所对应的圆心角的度数
(4)如果全年级共1000名同学,请你估算全年级对奥运知识 “了解较多”的学生人数.
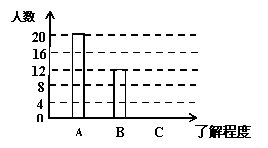
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com