1．若圆的半径为R，圆的面积为S，则S与R之间的函数关系式为(　 )

　　 A．S=2 R　　 B．S= R2　　 C．S=4 R2　　 D．S=

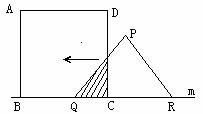
28．(13分)如图，有一边长为5cm的正方形ABCD和等腰△PQR，PQ=PR=5cm，QR=8cm，点B、C、Q、R在直线m上，当C、Q两点重合时，等腰△PQR以1cm/秒的速度沿直线m按箭头所示方向开始匀速运动，t秒后正方形ABCD与等腰△PQR重合部分的面积为S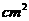。(1)当t=3秒时，求S的值；(2)当t=5秒时，求S的值；(3)当5秒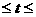8秒时，求S与t的函数关系式，并求出S的最大值。

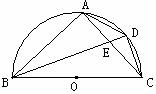
27．(13分)如图，BC为半圆的直径，O为圆心，D为AC的中点，四边形ABCD的对角线AC、BD相交于点E。

(1)△ABE与△DBC相似吗？请说明理由；

(2)若BC=5，CD=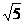，求sin∠AEB的值；

(3)在(2)的条件下求弦AB的长。

26．(12分)△ABC为如图15所示的平面直角坐标系中的格点三角形。

(1)将△ABC向x轴负半轴方向平移4个单位得到△A₁B₁C₁，画出图形并写出点A₁的坐标；

(2)以原点O为旋转中心，将△ABC顺时针旋转90°得到△A₂B₂C₂，画出图形并写出点A₂的坐标。

25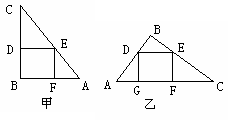．(8分)有一块直角三角形木板ABC，∠B=90º，AB=，面积为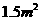，工人师傅要把它加工成一个面积最大的正方形桌面。请甲、乙两位同学进行设计方案，甲设计的方案如图甲所示，乙设计的方案如图乙所示。你认为哪位同学的设计方案符合要求？试说明理由(加工损耗忽略不计)。

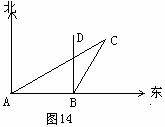
24．(8分)如图14，某船以每小时36海里的速度向正东航行，在A点测得某岛C在北偏东60º方向上，航行半小时后到达B点，此时测得岛C在北偏东30º方向上，已知该岛周围16海里内有暗礁。

　 (1)试说明B点是否在暗礁区域外？

　 (2)若继续向东航行，船有无触礁危险？请说明理由。

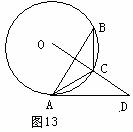
23．(8分)如图13，△ABC内接于⊙O，点D在OC的延长线上，且∠B=∠CAD=30º，试判定AD与⊙O的位置关系，并说明理由。

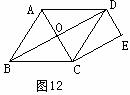
22．(8分)如图12，菱形ABCD的对角线AC、BD相交于点O，DE∥AC，CE∥BD。

求证：四边形CODE是矩形。

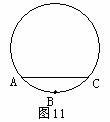
21．(8分)图11是某公园新建的圆形人工湖。为测量该湖的半径，小强和小丽沿湖边选取A、B、C三根木桩，使得A、B之间的距离与B、C之间的距离相等，并测得B到AC的距离为3米，AC的长为60米，请你帮他们求出人工湖的半径。

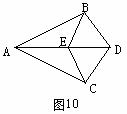
20．(8分)如图10，点E是AD上一点，AB=AC，

　(1)请你添加一个条件，使图中存在全等三角形，所添加的条件为　　　　　　　　　 ，你得到的一对全等三角形是△　　　 ≌△　　　 ；

　(2)证明(1)中的结论。