
题目列表(包括答案和解析)
6.(08山东滨州)若A(-4,y1),B(-3,y2),C(1,y3)为二次函数y=x2+4x-5的图象上的三点,则y1,y2,y3的大小关系是( )
A.y1<y2<y3 B.y2<y1<y3 C.y3<y1<y2 D.y1<y3<y2
5、(08吉林长春)二次函数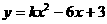 的图象与
的图象与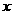 轴有交点,则
轴有交点,则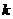 的取值范围是[ ]
的取值范围是[ ]
A.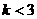 B.
B. C.
C.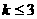 D.
D.
4、(08吉林长春)抛物线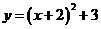 的顶点坐标是 [ ]
的顶点坐标是 [ ]
A.(-2,3) B.(2,3) C.(-2,-3) D.(2,-3)
3、已知二次函数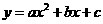 (其中
(其中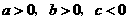 ),
),
关于这个二次函数的图象有如下说法:
①图象的开口一定向上;
②图象的顶点一定在第四象限;
③图象与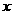 轴的交点至少有一个在
轴的交点至少有一个在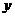 轴的右侧.
轴的右侧.
以上说法正确的个数为( )
A.0 B.1 C.2 D.3
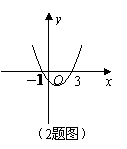
2.(08四川达州)已知二次函数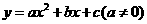 的图象如图所示,当
的图象如图所示,当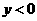 时,
时,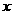 的取值范围是( )
的取值范围是( )
A.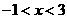 B.
B.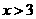
C.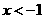 D.
D.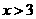 或
或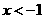
1.(08资阳) 在平面直角坐标系中,如果抛物线y=2x2不动,而把x轴、y轴分别向上、向右平移2个单位,那么在新坐标系下抛物线的解析式是 ( )
A.y=2(x-2)2 + 2 B.y=2(x + 2)2-2
 C.y=2(x-2)2-2 D.y=2(x + 2)2
+ 2
C.y=2(x-2)2-2 D.y=2(x + 2)2
+ 2
25.(12分)如图1所示,在 中,
中, ,
, ,
, 为
为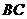 的中点,动点
的中点,动点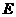 在
在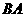 边上自由移动,动点
边上自由移动,动点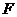 在
在 边上自由移动.
边上自由移动.


(1)点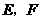 的移动过程中,
的移动过程中,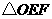 是否能成为
是否能成为 的等腰三角形?若能,请指出
的等腰三角形?若能,请指出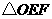 为等腰三角形时动点
为等腰三角形时动点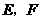 的位置.若不能,请说明理由.
的位置.若不能,请说明理由.
(2)当 时,设
时,设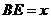 ,
,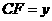 ,求
,求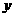 与
与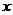 之间的函数解析式,写出
之间的函数解析式,写出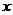 的取值范围.
的取值范围.
(3)在满足(2)中的条件时,若以 为圆心的圆与
为圆心的圆与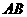 相切(如图2),试探究直线
相切(如图2),试探究直线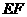 与
与 的位置关系,并证明你的结论.
的位置关系,并证明你的结论.
24.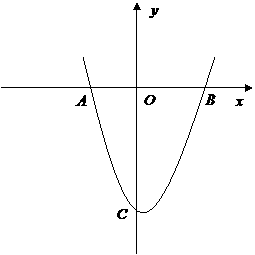 (10分)如图,已知二次函数
(10分)如图,已知二次函数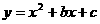 的图象经过点
的图象经过点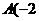 ,
, )、
)、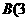 ,
, ),与
),与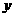 轴交于点
轴交于点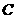 .
.
(1)求该二次函数的解析式;
(2)如在线段 上有一点
上有一点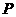 ,且点
,且点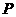 到点
到点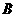 的
的
距离为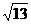 ,那么在
,那么在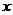 轴上是否存在点
轴上是否存在点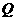 ,使以点
,使以点 、
、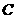 、
、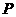 、
、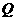 为顶点的四边形是梯形?如存在,请求出点
为顶点的四边形是梯形?如存在,请求出点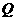 的坐标;如不存在,请说明理由.
的坐标;如不存在,请说明理由.
23.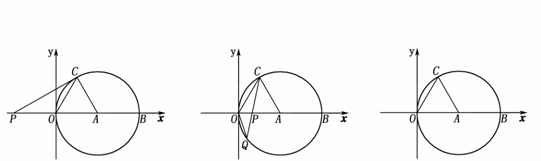 (8分)如图①,②,在平面直角坐标系
(8分)如图①,②,在平面直角坐标系 中,点
中,点 的坐标为(4,0),以点
的坐标为(4,0),以点 为圆心,4为半径的圆与
为圆心,4为半径的圆与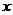 轴交于
轴交于 ,
,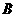 两点,
两点, 为弦,
为弦,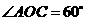 ,
,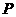 是
是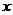 轴上的一动点,连结
轴上的一动点,连结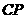 .
.
(1)求 的度数;(2分)
的度数;(2分)
(2)如图①,当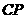 与
与 相切时,求
相切时,求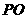 的长;(3分)
的长;(3分)
(3)如图②,当点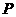 在直径
在直径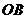 上时,
上时,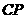 的延长线与
的延长线与 相交于点
相交于点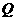 ,问
,问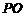 为何值时,
为何值时, 是等腰三角形?(3分)
是等腰三角形?(3分)
22. (8分)如图22,某学校九年级数学兴趣小组组织一次数学活动.在一座有三道环形路的数字迷宫的每个进口处都标记着一个数,要求进入者把自己当做数“1”,进入时必须乘进口处的数,并将结果带到下一个进口,依次累乘下去,在通过最后一个进口时,只有乘积是5的倍数,才可以进入迷宫中心,现让一名5岁小朋友小军从最外环任一个进口进入.
(8分)如图22,某学校九年级数学兴趣小组组织一次数学活动.在一座有三道环形路的数字迷宫的每个进口处都标记着一个数,要求进入者把自己当做数“1”,进入时必须乘进口处的数,并将结果带到下一个进口,依次累乘下去,在通过最后一个进口时,只有乘积是5的倍数,才可以进入迷宫中心,现让一名5岁小朋友小军从最外环任一个进口进入.
(1)小军能进入迷宫中心的概率是多少?请画出树状图进行说明.
(2)小组两位组员小张和小李商量做一个小游戏,以猜测小军进迷宫的结果比胜负.游戏规则规完:小军如果能进入迷宫中心,小张和小李各得1分;小军如果不能进入迷宫中心,则他在最后一个进口处所得乘积是奇数时,小张得3分,所得乘积是偶数时,小李得3分,你认为这个游戏公平吗?如果公平,请说明理由;如果不公平,请在第二道环进口处的两个数中改变其中一个数使游戏公平.
(3)在(2)的游戏规则下,让小军从最外环进口任意进入10次,最终小张和小李的总得分之和不超过28分,请问小军至少几次进入迷宫中心?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com