
题目列表(包括答案和解析)
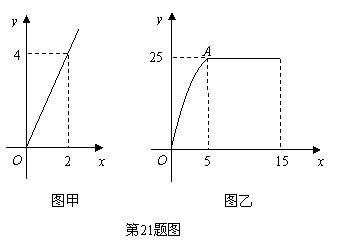
21、(2008 青海)王亮同学善于改进学习方法,他发现对解题过程进行回顾反思,效果会更好.某一天他利用30分钟时间进行自主学习.假设他用于解题的时间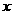 (单位:分钟)与学习收益量
(单位:分钟)与学习收益量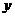 的关系如图甲所示,用于回顾反思的时间
的关系如图甲所示,用于回顾反思的时间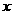 (单位:分钟)与学习收益量
(单位:分钟)与学习收益量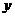 的关系如图乙所示(其中
的关系如图乙所示(其中 是抛物线的一部分,
是抛物线的一部分, 为抛物线的顶点),且用于回顾反思的时间不超过用于解题的时间.
为抛物线的顶点),且用于回顾反思的时间不超过用于解题的时间.
(1)求王亮解题的学习收益量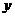 与用于解题的时间
与用于解题的时间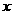 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量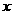 的取值范围;
的取值范围;
(2)求王亮回顾反思的学习收益量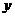 与用于回顾反思的时间
与用于回顾反思的时间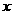 之间的函数关系式;
之间的函数关系式;
(3)王亮如何分配解题和回顾反思的时间,才能使这30分钟的学习收益总量最大?
(学习收益总量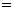 解题的学习收益量
解题的学习收益量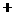 回顾反思的学习收益量)
回顾反思的学习收益量)
20.(08兰州)一座拱桥的轮廓是抛物线型(如图所示),拱高6m,跨度20m,相邻两支柱间的距离均为5m.
(1)将抛物线放在所给的直角坐标系中(如图所示),求抛物线的解析式;
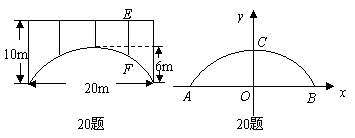 (2)求支柱
(2)求支柱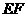 的长度;
的长度;
(3)拱桥下地平面是双向行车道(正中间是
一条宽2m的隔离带),其中的一条行车道能
否并排行驶宽2m、高3m的三辆汽车(汽车
间的间隔忽略不计)?请说明你的理由.
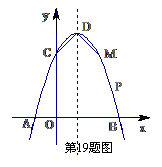
19、(08 山东临沂)如图,已知抛物线与x轴交于A(-1,0)、B(3,0)两点,与y轴交于点C(0,3)。
⑴求抛物线的解析式;
⑵设抛物线的顶点为D,在其对称轴的右侧的抛物线上是否存在点P,使得△PDC是等腰三角形?若存在,求出符合条件的点P的坐标;若不存在,请说明理由;
⑶若点M是抛物线上一点,以B、C、D、M为顶点的四边形是直角梯形,试求出点M的坐标。

18. (08徐州)已知二次函数的图象以A(-1,4)为顶点,且过点B(2,-5)
①求该函数的关系式;
②求该函数图象与坐标轴的交点坐标;
③将该函数图象向右平移,当图象经过原点时,A、B两点随图象移至A′、B′,
求△O A′B′的面积
17、(08广东梅州)如图所示,E是正方形ABCD的边AB上的动点, EF⊥DE交BC
于点F.(1)求证: 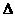 ADE∽
ADE∽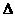 BEF;
BEF;
(2)设正方形的边长为4, AE=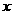 ,BF=
,BF=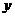 .当
.当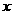 取什么值时,
取什么值时, 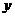 有最大值?并求出这个最大值.
有最大值?并求出这个最大值.
(二)二次函数的应用
10.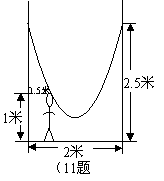 (08山西)二次函数
(08山西)二次函数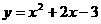 的图象的对称轴是直线 。
的图象的对称轴是直线 。
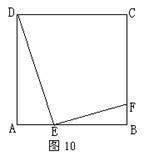
11、(2008四川内江)如图,小明的父亲在相距2米的两棵树间拴了一根绳子,给他做了一个简易的秋千,拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为 米.
12、(08年庆阳)二次函数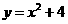 的最小值是
.
的最小值是
.
13、(08吉林长春)某商店经营一种水产品,成本为每千克40元的水产品,据市场分析,若按每千克50元销售,一个月能售出500千克;销售价每涨1元,月
销售量就减少10千克,针对这种水产品的销售情况,销售单价定为 元时,获得的利润最多.
14.初三数学课本上,用“描点法”画二次函数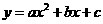 的图象时,列了如下表格:
的图象时,列了如下表格:
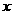 |
… |
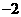 |
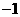 |
0 |
1 |
2 |
… |
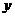 |
… |
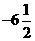 |
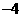 |
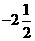 |
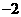 |
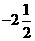 |
… |
根据表格上的信息回答问题:该二次函数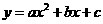 在
在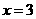 时,
时,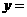 .
.
15.(08白银)抛物线 y=x2+x-4与y轴的交点坐标为 .
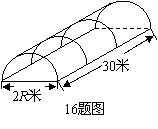
16.(08甘肃兰州)农村常需要搭建截面为半圆形的全封闭蔬菜塑料暖房如图所示,则需要塑料布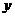 (m2)与半径
(m2)与半径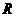 (m)的函数关系式是(不考虑塑料埋在土里的部分) .
(m)的函数关系式是(不考虑塑料埋在土里的部分) .

9、(08 河北)如图,正方形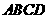 的边长为10,四个全等的小正方形的对称中心分别在正方形
的边长为10,四个全等的小正方形的对称中心分别在正方形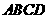 的顶点上,且它们的各边与正方形
的顶点上,且它们的各边与正方形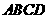 各边平行或垂直.若小正方形的边长为
各边平行或垂直.若小正方形的边长为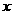 ,且
,且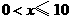 ,阴影部分的面积为
,阴影部分的面积为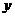 ,则能反映
,则能反映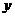 与
与 之间函数关系的大致图象是( )
之间函数关系的大致图象是( )


8.(08江苏镇江)福娃们在一起探讨研究下面的题目:

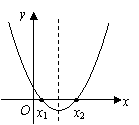
参考下面福娃们的讨论,请你解该题,你选择的答案是( )



 贝贝:我注意到当
贝贝:我注意到当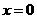 时,
时,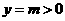 .
.
晶晶:我发现图象的对称轴为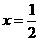 .
.
 欢欢:我判断出
欢欢:我判断出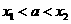 .
.
迎迎:我认为关键要判断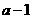 的符号.
的符号.
妮妮: 可以取一个特殊的值.
可以取一个特殊的值.
7.(08吉林长春)已知反比例函数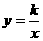 的图象如下右图所示,则二次函数
的图象如下右图所示,则二次函数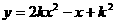 的图象大致为[ ]
的图象大致为[ ]
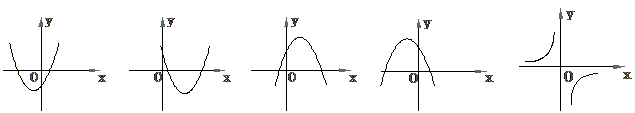
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com