
题目列表(包括答案和解析)
5.(2003·黑龙江)写出满足方程x+2y=9的一对整数值________________。
4.(2003·河南)如果二元一次方程组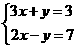 的解是关于某个一元二次方程的两个根,则这个一元二次方程是_____________________。
的解是关于某个一元二次方程的两个根,则这个一元二次方程是_____________________。
3.(2003·河南)若点P(a+b,-5)与(1,3a-b)关于原点对称,则关于x的二次三项式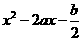 可以分解为____________________。
可以分解为____________________。
2.(2003·河南)若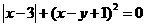 ,计算
,计算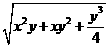 =_______。
=_______。
1.(2004·宁波)已知x+y=5,且x-y=1,则xy=_________。
3.(2003·陕西)为保护生态环境,我省某山区县响 国家“退耕还林”号召,将该县某地一部分耕地改为林地,改变后,林地面积和耕地面积共有180 平方千米,耕地面积是林地面积的25%,为求改变后林地面积和耕地面积各为多少平方千米,设耕地面积为x平方千米,林地面积为y平方千米,根据题意,列出如下四个方程组,其中正确的是( )
A.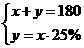 B.
B.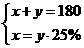 ; C.
; C.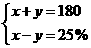 D.
D.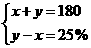
2.(2003·南宁)下列方程组的解中是二元一次方程组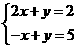 的解是( )
的解是( )
A.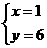 B.
B.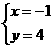 C.
C.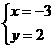 D.
D.
1.(2004·呼和浩特)某商店有两个进价不同的计算器都卖了64元,其中一个盈利60%,另一个亏本20%,在这项买卖中,这家商店( )
A.赔了8元 B.赚了32元 C.不赔不赚 D.赚了8元
题型一 方程组解的判定
例1(2003·南宁)已知二元一次方程组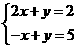 的解是( )
的解是( )
A.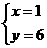 B.
B.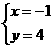 C.
C.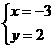 D.
D.
分析:本题有两种解法:一种是解方程组,求出其解;另一种是将被选答案代入方程组,逐个验证。
答案:B
题型二 求待定系数或代数式的值
例2(2001·湖南邵阳)已知二元一次方程组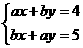 的解是
的解是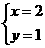 ,则a+b的值为________。
,则a+b的值为________。
分析:根据方程组的定义,把x=2,y=1代入方程组,转化为关于a、b的方程组,解出a与b的值,问题就解决了,也可应用整体思想,直接求出a+b的值。
解法1:把x=2,y=1代入方程组,
得
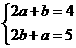 解得
解得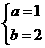
∴a+b=3
解法2:把x=2,y=1代入原方程组,
得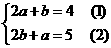
(1)+(2)得3(a+b)=9,∴a+b=3
点评:运用整体思想巧求代数式的值是中考常考内容,解题时,注意观察方程组的特点,灵活运用方程组的变形技巧而进行合理、正确的解答。
 题型三 解方程组
题型三 解方程组
例3 (2004·芜湖)解方程组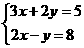
分析:因为y的系数绝对值是1,所以用代入消元法解较简单。
解:由②,得y=2x-8 ③
把③代入①,得3x+2(2x-8)=5
3x+4x-16=5
∴x=3
把x=3代入③,得y=2×3-8=-2
∴方程组的解为 x=3 y=-2
点评:解方程组要善于观察方程组的特点,灵活选用适当的方法,提高解题速度。
题型四 列方程组解应用题
例4(2004·北京)某山区有23名中、小学生因贫困失学需要捐助, 资助一名中学生的学习费用需要a元,一名小学生的学习费用需要b元,某校学生积极捐款,初中各年级学生捐款数额与用其恰好捐助贫困中学生和小学生人数的部分情况如下表:
|
|
初一年级 |
初二年级 |
初三年级 |
|
捐款数额(元) |
4000 |
4200 |
7400 |
|
捐助贫困学生(名) |
2 |
3 |
|
|
捐助贫困小学生人数(名) |
4 |
3 |
|
(1)求a、b的值;
(2)初三年级学生的捐款解决了其余贫困中小学生的学习费用, 请将初三年级学生可捐助的贫困中、小学生人数直接填入上表中。(不需写出计算过程)
分析:本题存在两个等量关系,分别是捐助2名中学生的学习费用+4 名小学生的学习费用=4000和捐助3名中学生的学习费用+3名小学生的学习费用=4200。
解:(1)根据题意,得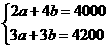
解这个方程组,得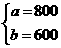
(2)初三年级学习捐助贫困中学生人数为4(名), 捐助贫困小学生人数为7(名)。
基础达标验收卷
3.二元一次方程组的应用
列二元一次方程组的关键是能正确分析出题目中的等量关系,题目内容往往与生活实际相贴近,与社会关系的热点问题相联系,请平时注意搜集、观察与分析。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com