4.(2003.江西)如图,∠1+∠2+∠3+∠4=_________.

3.(2003.吉林省)如图,∠1+∠2+∠3+∠4=________.

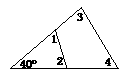
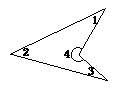
　　　　　　　　　　　 (第3题)　　　　　　　　　　 (第4题)

2.(2004.贵阳市)正n边形的内角和等于1 080 °, 那么这个正n 边形的边数n=______.

1.(2004.哈尔滨市)一个多边形的每一个外角都等于36°,则该多边形的内角和等于____.

5.(2003.山西)有若干张如图所示的正方形和长方形卡片

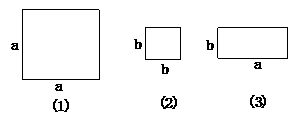
表中所列四种方案能拼成边长为(a+b)的正方形的是(　 )

卡片数量张 　 方案	(1)	(2)	(3)
A	1	1	2
B	1	1	1
C	1	2	1
D	2	1	1

4.(2004.天津市)若一个正多边形的每一个内角都等于120°,则它是(　 )

A.正方形　　 B.正五边形　　 C.正六边形　　 D.正八边形

3.(2004.昆明市)如图是中国共产主义青年团团旗上的图案,点A、B、C、D、E五等分圆,则∠A+∠B+∠C+∠D+∠E的度数是(　 　)

A.180°　　 B.150°　　 C.135°　　 D.120°

2.(2003.福建泉州)如果只用正三角形作平面镶嵌(要求镶嵌的正三角形的边与另一个正三角形的边重合),则在它的每一个顶点周围的正三角形的个数为(　 ).

A.3　　　 B.4　　 C.5　　 D.6

1.(2003.新疆)某人到瓷砖商店去购买一种正多边形的瓷砖,铺设无缝地板, 他购买的瓷砖形状不可以是(　 ).

A.正三角形　　 B.正四边形　　 C.正六边形　　 D.正八边形

题型一　 平面镶嵌问题

例1　 (2004.武汉市)一幅美丽的图案, 在某个顶点处由四个边长相等的正多边形镶嵌而成,其中的三个分别为正三边形、正四边形、正六边形,那么另外一个为(　 )

A.正三边形　　 B.正六边形　 C.正五边形　　 D.正六边形

解析:正三角形的一个内角等于60°,正四边形的一个内角等于90°, 正六边形的一个内角等于120°,而60°+90°+120°+90°=360°, 所以另一个只能取正四边形.

答案:B.

例2 　(2004.福州市)下列图形中能够用来作平面镶嵌的是(　 )

A.正八边形　 B.正七边形　 C.正六边形　 D.正五边形

解析:要使用同一种正多边形作平面镶嵌,必须满足正多边形的几个内角之和为360°,正多边形中只有正三角形,正方形和正六边形满足这个条件,其他的正多边形都不满足.

答案:C

点评:正确理解正三角形、正方形、正六边形乃至任意三角形、 四边形能镶嵌平面的理由，是解决这类问题的关键。

题型二　 三角形三边关系的应用

例3　 (2004.哈尔滨市)以下列各组线段长为边,能组成三角形的是(　 )

A.1cm,2cm,4cm　　 B.8cm,6cm,4cm;　　 C.12cm,5cm,6cm　　 D.2cm,3cm,6cm

解析:根据三角形三边关系定理,即可得证.

答案:B.

题型三　 多边形的内角和、外角和定理的应用

例4　 (2003.全国初中数学联赛题)在凸十边形的所有内角中, 锐角的个数最多是(　 )

A.0　　 B.1　　 C.3　　 D.5

解析:因为多边形的外角和是一个和边数无关的定值,这个问题可从外角的角度来考查.如果多边形的内角中有3个以上是锐角,则与它们相邻的外角中就有3个以上是钝角,外角和将超过360°.

答案:C.

例5　 (2003.北京海淀区)如图,把△ABC纸片沿DE折叠,当点A 落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变. 请试着找一找这个规律,你发现的规律是(　 )

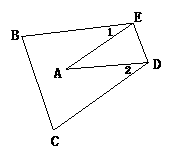A.∠A=∠1+∠2　　 B.2∠A=∠1+∠2;　　

C.3∠A=2∠1+∠2　 D.3∠A=∠1+2∠2

解析:由题意可知∠AED=,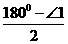

∠ADE=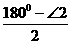 ,所以由三角形的内角和等于180°, 即可找到∠A与∠1+∠2的关系.

答案:B.

点评:转化思想是一种重要的数学方法,它能化难为易,化未知为已知,掌握这种方法,对我们学习数学有很大帮助.

基础达标验收卷