1．3的倒数是(　　 )

A．　　　　　 B．　　　　　 C．　　　　　　 D．

4.一个多边形,少去一个内角外,其余各内角的和为1 700°,求这个多边形的边数?

3.三角形的两边长是4cm与8cm,它的周长是一个奇数,这样的三角形的周长有几种不同的长度?

2.给你4根木棒,它们的长度分别是2cm,3cm,4cm和5cm,任取其中三根,可组成几种不同的三角形?

1.在日常生活中,观察各种建筑物的地板,就能发现地板常用各种正多边形地砖铺砌成美丽的图案,也就是说,使用给定的某些正多边形,能够拼成一个平面图形,既不留一丝空白,又不互相重叠(在数学上叫做平面镶嵌),这显然与正多边形的内角大小有关,当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个周角(360°)时,就拼成了一个平面图形.

(1)请你根据图中的图形,填写表中空格:

(2)如果限于用一种正多边形镶嵌,哪几种正多边形能镶嵌成一个平面图形?

(3)从正三角形、正四边形、正六边形中选一种,再在其他正多边形中选一种, 请画出用这两种不同的正多边形镶嵌成一个平面图形, 并探索这两种正多边形共能镶嵌成几种不同的平面图形?说明你的理由.

4.(2003.甘肃)某地板厂要制作一批正六边形形状的地板砖,为适应市场多样化需求,要求在地板砖上设计的图案能够把正六边形6等分,请你帮他们设计等分图案(至少设计两种).

能力提高练习

3.(“希望杯”初二数学竞赛题)一个凸多边形有且仅有4个内角是钝角,这样的多边形的边数最多有几条?

2.(山东省数学竞赛题)在凸n边形中,小于108°的角最多可以有几个?

1.(“祖冲之杯”数学邀请赛题)一个凸多边形的每一个内角都等于140°,那么从这个多边形的一个顶点出发的对角线的条数是多少?

5.(2003.江西)用黑白两种颜色的正六边形地面砖按如图所示的规律, 拼成若干个图案.

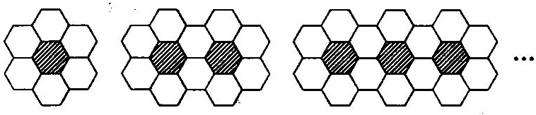
第1个　　　　　 第2个　　　　　　　　　　　　 第3个

(1)第4个图案中有白色地面砖______块;

(2)第n个图案中有白色地面砖______块.