4.反比例函数经常与一次函数、二次函数等知识相联系.

3.反比例函数y=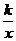中k的意义

注意:反比例函数y=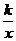 (k≠0)中比例系数k的几何意义,即过双曲线y=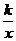(k≠0)上任意一点引x轴、y轴垂线,所得矩形面积为│k│.

2.反比例函数的图象

在用描点法画反比例函数y=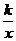的图象时,应注意自变量x的取值不能为0,应从1或-1开始对称取点.

1.反比例函数的概念

反比例函数y=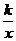中的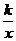是一个分式,自变量x≠0,函数与x轴、y轴无交点,y=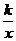也可写成y=kx^-1(k≠0),注意自变量x的指数为-1, 在解决有关自变量指数问题时应特别注意系数k≠0这一限制条件.

3.反比例函数性质;　　　　 4.待定系数法确定函数解析式.

1.反比例函数意义;　　　　 2.反比例函数 反比例函数图象;

例4 (四川省)如图5，在⊙O中，AB、AC是互相垂直的两条弦， AB＝8cm，AC＝6cm，那么⊙O的半径OA的长(　　 )

A．4 cm　　 B．5 cm　　　 C．6 cm　　 D．8 cm

[分析]要求半径OA的长，可通过垂径定理构造Rt△，于是过O分别作OD⊥AB，OE⊥AC，则可得矩形ADOE。

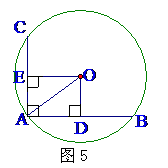解：如图5，过O分别作OD⊥AB于D，OE⊥AC于E，

则得矩形ADOE，∴ OD＝AE，

又∵ AD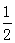＝AB＝4，OD＝AE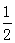＝AC＝3；

　∴ AO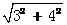＝＝5cm．故选(B)．

本资料由《七彩教育网》 提供！

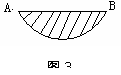例3 (长春市)某居民小区一处圆柱形的输水管道破裂，维修人员为更换管道，需确定管道圆形截面的半径，图3是水平放置的破裂管道有水部分的截面．

(1)请你补全这个输水管道的圆形截面；

(2)若这个输水管道有水部分的水面宽AB＝16cm，水面最深地方的高度为4cm，求这个圆形截面的半径．

分析：(1)要补全输水管道的圆形截面，需要画出图3所在的圆，因此首先确定所在圆的圆心和半径.⑴任作两条弦，⑵分别作出两弦的垂直平分线，⑶两弦的垂直平分线的交点为圆心，⑷以交点为圆心,交点到圆上任意一点为半径作圆，所作出的圆即为所求.作图过程:略.

(2)本题的解题关键是作垂直于弦的半径,然后构造直角三角形,应用勾股定理列方程求解.

解：(1)正确作出图形，并做答．

(2)如图4,解：过O作OC⊥AB于D ，交弧AB于C，

∵OC⊥AB ， ∴BD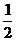＝AB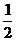＝×16＝8cm．

由题意可知，CD＝4cm．

设半径为x Cm，则OD＝(x－4)cm．

在Rt△BOD 中，由勾股定理得：

OD²+BD²＝OB²， ∴( x－4)²+8²＝x²．

∴x＝10．

例2 (南京市)如图2，矩形ABCD与与圆心在AB上的⊙O交于点G、B、F、E，　 GB＝8cm，AG＝1cm，DE＝2cm，则EF＝ 　　　　cm .

[分析]本题上手有点不知所措，其实利用矩形和垂径定理相关知识可以得到解决。分别过O，G作OM⊥CD，GN⊥DC，即可求出EF的长。

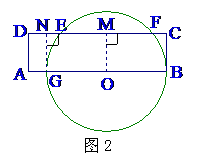解：如图2，分别过O，G作OM⊥CD，GN⊥DC，则根据矩形的性质可得：NC＝GB＝8，DN＝AG＝1，GN∥OM∥BC，

　 ∵ OM⊥EF，　 ∴ EM＝MF，

　 ∵ OG＝OB，GN∥OM∥BC，　 ∴ MN＝MC，

　 ∴ CF＝NE，　 ∵ DE＝2，∴ NE＝DE－DN＝DE－AG＝1，

　 ∴ EF＝NC－NE－CF＝8－2＝6．