
题目列表(包括答案和解析)
7.


 (2002.青岛)已知关于x的函数y=k(x-1)和y=-
(2002.青岛)已知关于x的函数y=k(x-1)和y=-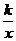 (k≠0),它们在同一坐标系内的图象大致是下图中的( )
(k≠0),它们在同一坐标系内的图象大致是下图中的( )
6.(2004·武汉)已知直线y=kx+b与双曲线y=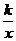 交于A(x1,y1),B(x2,y2) 两点, 则x1·x2的值( )
交于A(x1,y1),B(x2,y2) 两点, 则x1·x2的值( )
A.与k有关、与b无关; B.与k无关、与b无关; C.与k、b都有关; D.与k、b都无关
5.(2004·上海)在函数y=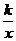 (k>0)的图象上有三点A1(x1,y1),A2(x2,y2),A3( x3.y3),已知x1<x2<0<x3,则下列各式中,正确的是( )
(k>0)的图象上有三点A1(x1,y1),A2(x2,y2),A3( x3.y3),已知x1<x2<0<x3,则下列各式中,正确的是( )
A.y1<0<y3 B.y3<0<y1; C.y2<y1<y3 D.y3<y1<y2
4. (2004·徐州)如图,点P是x轴上的一个动点,过点P作x轴的 垂线PQ交双曲线于点Q,连结OQ,当点P沿x轴正半方向运动时,Rt△QOP的面积( )
(2004·徐州)如图,点P是x轴上的一个动点,过点P作x轴的 垂线PQ交双曲线于点Q,连结OQ,当点P沿x轴正半方向运动时,Rt△QOP的面积( )
A.逐渐增大; B.逐渐减小; C.保持不变; D.无法确定
3.(2003·广东)如图,某个反比例函数的图象经过点P,则它的解析式为( )
A.y=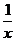 (x>0); B.y=-
(x>0); B.y=-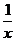 (x>0)C.y=
(x>0)C.y=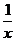 (x<0); D.y=-
(x<0); D.y=-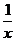 (x<0)
(x<0)
2.
 (2003·江西)反比例函数y=-
(2003·江西)反比例函数y=-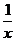 的图象大致是( )
的图象大致是( )

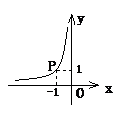
1.(2004·沈阳)经过点(2,-3)的双曲线是( )
A.y=-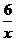 B.
B.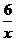 C.y=
C.y=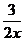 D.-
D.-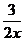
3.反比例函数的应用
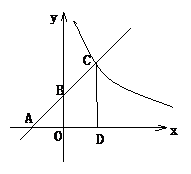 例4 (2003·天津)如图所示,已知一次函数y=kx+b(k≠0)的图象与x 轴、y轴分别交于A、B两点,且与反比例函数y=
例4 (2003·天津)如图所示,已知一次函数y=kx+b(k≠0)的图象与x 轴、y轴分别交于A、B两点,且与反比例函数y=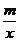 (m≠0)的图象在第一象限交于C点, CD垂直于x轴,垂足为D.若OA=OB=OD=1,
(m≠0)的图象在第一象限交于C点, CD垂直于x轴,垂足为D.若OA=OB=OD=1,
(1)求点A、B、D的坐标;
(2)求一次函数和反比例函数的解析式.
分析:(1)由OA=OB=OD=1可确定A、B、D三点坐标.
(2)将A、B两点坐标分别代入y=kx+b,可用待定系数法确定一次函数的解析式, 由C点在一次函数的图象上可确定C点坐标,将C点坐标代入y=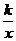 可确定反比例函数的解析式.
可确定反比例函数的解析式.
解:(1)∵OA=OB=OD=1,∴点A、B、D的坐标分别为A(-1,0),B(0,1),C(1,0).
(2)∵点A、B在一次函数y=kx+b(k≠0)的图象上,
∴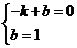 ,解得
,解得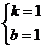 ,
,
∴一次函数的解析式为y=x+1.
∵点C在一次函数y=x+1的图象上,且CD⊥x轴,
∴点C的坐标为(1,2) .
又∵点C在反比例函数y=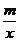 (m≠0)的图象上,m=2.
(m≠0)的图象上,m=2.
∴反比例函数的解析式为y=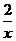 .
.
基础达标验收卷
2.待定系数法确定函数解析式
例3 (2003·南充)已知y与x2成反比例,并且当x=-1时,y=2,那么当x=4时,y等于( )
A.-2 B.2
C.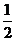 D.-4
D.-4
分析:已知y与x2成反比例,∴y=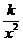 (k≠0).将x=-2,y=2代入y=
(k≠0).将x=-2,y=2代入y=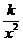 可求得k,从而确定双曲线解析式.
可求得k,从而确定双曲线解析式.
解:∵y与x2成反比例,∴y=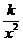 (k≠0).
(k≠0).
当x=-2时,y=2,∴2=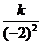 ,k=8
,k=8
∴y=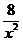 ,把x=4代入y=
,把x=4代入y=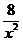 得y=
得y=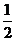 .
.
故答案为C.
点评:此题主要考查反比例函数概念及待定系数法确定函数解析式.
1.反比例函数的图象
例1
(2003·三明)函数y=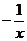 (x>0)的图象大致是( )
(x>0)的图象大致是( )


解析:函数y=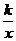 的图象是双曲线,当k<0时双曲线两分支分别在第二、四象限内, 而已知中(x>0)表明横坐标为正,故双曲线位于第四象限.
的图象是双曲线,当k<0时双曲线两分支分别在第二、四象限内, 而已知中(x>0)表明横坐标为正,故双曲线位于第四象限.
答案:D.
点评:本题主要考查反比例函数的图象.但需注意的是y=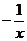 中的限制条件(x>0), 即双曲线的横坐标为正.
中的限制条件(x>0), 即双曲线的横坐标为正.



 例2 (2003·宜昌)函数y=kx+1与函数y=
例2 (2003·宜昌)函数y=kx+1与函数y=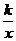 在同一坐标系中的大致图象是( )
在同一坐标系中的大致图象是( )
分析:明确一次函数y=kx+1中的k的含义与函数y=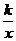 中k的含义是解题的关键.
中k的含义是解题的关键.
解:可用排除法,假设y=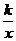 中k>0,双曲线过第一、三象限,则直线y=kx+1 也应过第一、第三象限且与y轴交于正半轴,故排除B、D.同理可排除C,故答案为A.
中k>0,双曲线过第一、三象限,则直线y=kx+1 也应过第一、第三象限且与y轴交于正半轴,故排除B、D.同理可排除C,故答案为A.
点评:解决同一坐标系中两种函数共存问题,首先明确同一字母系数在不同函数解析式中的含义,切勿出现“张冠李戴”的错误.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com