
题目列表(包括答案和解析)
3.化简求值题
例3 (1)(2003·菏泽)已知a+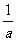 =5,则
=5,则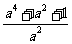 =________.
=________.
(2)(2002·南京)已知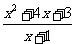 =0,先化简后求
=0,先化简后求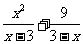 的值.
的值.
解:(1)将a+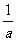 =5,两边平方得a2+2+
=5,两边平方得a2+2+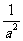 =25.
=25.
∴a2+2+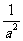 =23,
=23,
∴ =a2+1+
=a2+1+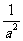 =a2+
=a2+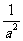 +1=24.
+1=24.
(2)∵ ,
,
∴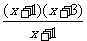 =0,
=0,
∴x+3=0.
∴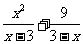 =
=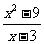 =x+3=0.
=x+3=0.
点评:善于观察发现已知条件与待求分式之间的关系是解决此类问题的关键.
基础达标验收卷
2.分式的基本性质的识别
例2 (2003·山西)下列各式与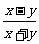 相等的是( )
相等的是( )
A.  ; B.
; B. 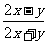 ;
C.
;
C. 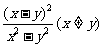 D.
D. 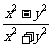
解析:根据分式的基本性质易发现C成立.
答案:C.
点评:分式的基本性质是一切分式运算的基础,分子与分母只能同乘以(或除以)同一个不等于零的整式,而不能同时加上(或减去)同一个整式.
1.识别分式的概念
例1 (2002·黑龙江)如果分式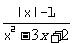 的值为零,那么x等于( )
的值为零,那么x等于( )
A.-1 B.1 C.-1或1 D.1或2
解析:要使分式的值为零,只需分子为零且分母不为零,
∴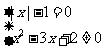 . 解得x=-1.
. 解得x=-1.
答案:A.
4.可化为一元一次方程的分式方程的应用
会根据具体情景列出分式方程,并会求解,注意验根这一步不可少.
3.会进行分式的四则运算
分式的四则运算主要出现在化简中,与通分、约分、分式的基本性质联合,要保证最后结果为最简分式.
2.分式基本性质的灵活应用
利用分式的基本性质熟练进行约分和通分,这是分式运算的基础,利用分式的基本性质时,要注意分子、分母同乘以和除以不为零的整式.
1.弄清分式有意义,无意义和值为零的条件
分式有意义的条件是分母不为零;无意义的条件是分母为零;值为零的条件是分子为零且分母不为零,弄懂这几个条件是做分式题很重要的一点.
┌───┬───────────┬────────────┐
│ │ │ 知识与技能目标 │
│ 考点 │ 课标要求 ├──┬──┬──┬───┤
│ │ │了解│理解│掌握│灵活应用
├───┼───────────┼──┼──┼──┼───┤
│ │ 分式 │ │ ∨ │ │ │
│ 分式 ├───────────┼──┼──┼──┼───┤
│ 的有 │ 有理式 │ │ ∨ │ │ │
│ 关概 ├───────────┼──┼──┼──┼───┤
│ 念 │ 最简分式 │ │ ∨ │ │ │
│ ├───────────┼──┼──┼──┼───┤
│ │ 最简公分母 │ │ ∨ │ │ │
├───┼───────────┼──┼──┼──┼───┤
│ │ 分式的基本性质 │ │ │ ∨ │ ∨ │
│ ├───────────┼──┼──┼──┼───┤
│ 分式 │ 分式的运算 │ │ │ ∨ │ ∨ │
│ ├───────────┼──┼──┼──┼───┤
│ │可化为一元一次方程的 │ │ │ │ ∨ │
│ │ 分式方程 │ │ │ │ │
└───┴───────────┴──┴──┴──┴───┘
分式
例5
计算 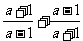 .
.
错解: =
=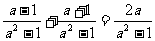 .
.
剖析:通分的依据是分式的基本性质:分子的分子、分母都乘以或除以一个不等于0的整式,分式的值不变.错解在违背了分式的基本性质,只把分式的分母乘以一个整式,而分子乘.这样所得的分式就与原分式不等值了.
正解: =
=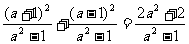 .
.
[说明]分式的加减运算的关键是通分,通分时要注意分式基本性质的理解及应用.
本资料由《七彩教育网》 提供!
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com