5.抛物线y=ax²+bx+c中a、b、c符号的确定

　　 a的符号由抛物线开口方向决定,当a>0时,抛物线开口向上;当a<0时,抛物线开口向下;c的符号由抛物线与y轴交点的纵坐标决定.当c>0时,抛物线交y轴于正半轴;当c<0时,抛物线交y轴于负半轴;b的符号由对称轴来决定.当对称轴在y轴左侧时,b的符号与a的符号相同;当对称轴在y轴右侧时,b的符号与a的符号相反;简记左同右异.

4.二次函数与一元二次方程的关系

　　 抛物线y=ax²+bx+c当y=0时抛物线便转化为一元二次方程ax²+bx+c=0,即抛物线与x轴有两个交点时,方程ax²+bx+c=0有两个不相等实根;当抛物线y=ax²+bx+c与x轴有一个交点,方程ax²+bx+c=0有两个相等实根;当抛物线y=ax²+bx+c与x轴无交点,方程ax²+bx+c=0无实根.

3.待定系数法是确定二次函数解析式的常用方法

　　 一般地,在所给的三个条件是任意三点(或任意三对x,y的值)可设解析式为y=ax²+bx+c,然后组成三元一次方程组来求解;在所给条件中已知顶点坐标或对称轴或最大值时,可设解析式为y=a(x-h)²+k;在所给条件中已知抛物线与x轴两交点坐标或已知抛物线与x轴一交点坐标和对称轴,则可设解析式为y=a(x-x₁)(x-x₂)来求解.

2.理解二次函数的性质

　　 抛物线的开口方向由a的符号来确定,当a>0时,在对称轴左侧y随x的增大而减小;在对称轴的右侧,y随x的增大而增大;简记左减右增,这时当x=-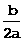时,y_最小值=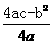;反之当a<0时,简记左增右减,当x=-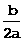时y_最大值=.

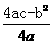1.二次函数的图象

　　 在画二次函数y=ax²+bx+c(a≠0)的图象时通常先通过配方配成y=a(x+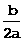)²+ 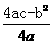的形式,先确定顶点(-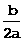,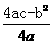),然后对称找点列表并画图,或直接代用顶点公式来求得顶点坐标.

　　 ┌───┬───────────┬────────────┐

　　 │　　　 │　　　　　　　　　　　 │　　 知识与技能目标　　 │

　　 │ 考点 │　　 考纲要求　　　　 ├──┬──┬──┬───┤

　　 │　　　 │　　　 　　　　　　　　│了解│理解│掌握│灵活应用

　　 ├───┼───────────┼──┼──┼──┼───┤

　　 │　　　 │理解二次函数的意义　　 │　　 │ ∨ │　　 │　　　 │

　　 │　　　 ├───────────┼──┼──┼──┼───┤

　　 │　　　 │会用描点法画出二次函数│　　 │　　 │　　 │　　　 │

　　 │　　　 │的图象　　　　　　　　 │　　 │　　 │ ∨ │　　　 │

　　 │　 二　 ├───────────┼──┼──┼──┼───┤

　　 │　　　 │会确定抛物线开口方向、│　　 │　　 │ ∨ │　　　 │

　　 │　 次　 │顶点坐标和对称轴　　　 │　　 │　　 │　　 │　　　 │

　　 │　　　 ├───────────┼──┼──┼──┼───┤

　　 │　 函　 │通过对实际问题的分析确│　　 │　　 │　　 │　　　 │

　　 │　　　 │定二次函数表达式　　　 │　　 │ ∨ │ ∨ │　　 　│

　　 │　 数　 ├───────────┼──┼──┼──┼───┤

　　 │　　　 │理解二次函数与一元二次│　　 │　　 │　　 │　　　 │

　　 │　　　 │方程的关系　　　　　　 │　　 │ ∨ │　　 │　　　 │

　　 │　　　 ├───────────┼──┼──┼──┼───┤

　　 │　　　 │会根据抛物线y=ax²+bx+c│　　 │　　 │　　 │　　　 │

　　 │　　　 │(a≠0)的图象来确定a、 │　　 │　　 │ ∨ │　　　 │

　　 │　　　 │b、c的符号　　　　　　 │　　 │　　 │　　 │　　　 │

　　 └───┴───────────┴──┴──┴──┴───┘

6.抛物线y=ax²+bx+c的图象与a、b、c之间的关系。

5.二次函数与一元二次方程的关系。

4.二次函数 待定系数法确定函数解析式　 一般式：y=ax²+bx+c(a≠0)

　　　　　　　 　　　　　　　　　　　两根式：y=a(x-x₁)(x-x₂)(a≠0)

1.二次函数的意义;2.二次函数的图象;3.二次函数的性质

　　　　　　　　　　　　　 顶点式：y=a(x-h)²+k(a≠0)