1.(2004·河北)若将二次函数y=x²-2x+3配方为y=(x-h)²+k的形式,则 y=_______.

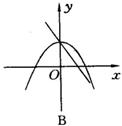
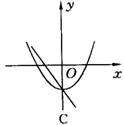
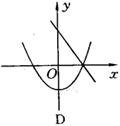
5.(2004·河北)在同一直角坐标系中,一次函数y=ax+c和二次函数y=ax²+c的图象大致为(　 ).

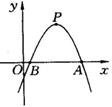　 6.(2004·昆明)已知二次函数y=ax²+bx+c(a≠0)图象的顶点P的横坐标是4,图象交x轴于点A(m,0)和点B,且m>4,那么AB的长是(　 ).

A.4+m　　 B.m　　　 C.2m-8　　　 D.8-2m

4.(2003·杭州)把抛物线y=x²+bx+c的图象向右平移3个单位,再向下平移2个单位,所得图象的解析式是y=x²-3x+5,则有(　 ).

　　 A.b=3,c=7　　　 B.b=-9,c=-15

C.b=3,c=3　　　 D.b=-9,c=21

2.(2004·重庆)二次函数y=ax²+bx+c的图象如图,则点M(b,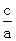)在(　 ).

　　 A.第一象限;　 B.第二象限;　 C.第三象限;　 D.第四象限

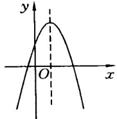　 3.(2004·天津)已知二次函数y=ax²+bx+c,且a<0,a-b+c>0,则一定有(　 ).

　 　A.b²-4ac>0　　　 B.b²-4ac=0

　　 C.b²-4ac<0　　　 D.b²-4ac≤0

1.(2003·大连)抛物线y=(x-2)²+3的对称轴是(　 ).

　　 A.直线x=-3　　　 B.直线x=3　　 C.直线x=-2　　　 D.直线x=2

4.　 二次函数的应用

　　 例5 　(2003·厦门)已知抛物线y=x²+(2k+1)x-k²+k,

　　 (1)求证:此抛物线与x轴总有两个不同的交点.

　　 (2)设x₁、x₂是此抛物线与x轴两个交点的横坐标,且满足x₁²+x₂²=-2k²+2k+1.

　　 ①求抛物线的解析式.

　　 ②设点P(m₁,n₁)、Q(m₂,n₂)是抛物线上两个不同的点,且关于此抛物线的对称轴对称.

　　 求m+m的值.

分析:(1)欲证抛物线与x轴有两个不同交点,可将问题转化为证一元二次方程有两个不相等实数根,故令y=0,证△>0即可.

(2)①根据二次函数的图象与x轴交点的横坐标即是一元二次方程的根.由根与系数的关系,求出k的值,可确定抛物线解析式;②由P、Q关于此抛物线的对称轴对称得n₁=n₂,由n₁=m₁²+m₁,n₂=m₂²+m₂得m₁²+m₁=m₂²+m₂,即(m₁-m₂)(m₁+m₂+1)=0可求得m₁+m₂=-1.

　　 解:(1)证明:△=(2k+1)²-4(-k²+k)

　　 =4k²+4k+1+4k²-4k=8k²+1.

　　 ∵8k²+1>0,

　　 即△>0,∴抛物线与x轴总有两个不同的交点.

　　 (2)①由题意得x₁+x₂=-(2k+1), x₁· x₂=-k²+k.

　　 ∵x₁²+x₂²=-2k²+2k+1,

　　 ∴(x₁+x₂)²-2x₁x₂=-2k²+2k+1,

　　 即(2k+1)²-2(-k²+k)=-2k²+k+1,

　　 4k²+4k+1+2k²-2k=-2k²+2k+1.

　　 ∴8k²=0,∴k=0,

　　 ∴抛物线的解析式是y=x²+x.

　　 ②∵点P、Q关于此抛物线的对称轴对称,

　　 ∴n₁=n₂.

　　 又n₁=m₁²+m_1,n₂=m₂²+m₂.

　　 ∴m₁²+m₁=m₂²+m₂,

　　 即(m₁-m₂)(m₁+m₂+1)=0.

　　 ∵P、Q是抛物上不同的点,

　　 ∴m₁≠m₂,即m₁-m₂≠0.

　　 ∴m₁+m₂+1=0

　　 即m₁+m₂=-1.

　 　点评:本题考查二次函数的图象(即抛物线)与x轴交点的坐标与一元二次方程根与系数的关系.二次函数经常与一元二次方程相联系并联合命题是中考的热点.

基础达标验收卷

3.　 二次函数的性质

　 　例4　 (2002·杭州)对于反比例函数y=-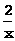与二次函数y=-x²+3,请说出他们的两个相同点:①_________,②_________;再说出它们的两个不同点:①________,②_________.

　 　分析:本小题是个开放性题目,可以从以下几点性质来考虑①增减性②图象的形状③最值④自变量取值范围⑤交点等.

　 　解:相同点:①图象都是曲线,②都经过(-1,2)或都经过(2,-1);

　　 不同点:①图象形状不同,②自变量取值范围不同,③一个有最大值,一个没有最大值.

　　 点评:本题主要考查二次函数和反比例函数的性质,有关函数开放性题目是近几年命题的热点.

2. 二次函数的图象

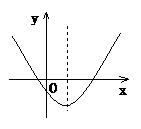　 　例2　 (2003·孝感)y=ax²+bx+c(a≠0)的图象如图所示,则点M(a,bc)在(  ).

　　 A.第一象限　　　 B.第二象限

　 　C.第三象限　　　 D.第四象限

　　 分析:由图可知:

　　 抛物线开口向上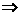a>0.

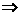　　 bc<0.

　　 ∴点M(a,bc)在第一象限.

　　 答案:A.

　　 点评:本题主要考查由抛物线图象会确定a、b、c的符号.

例3　 (2003·岳阳)已知一次函数y=ax+c二次函数y=ax²+bx+c(a≠0),它们在同一坐标系中的大致图象是(　 ).

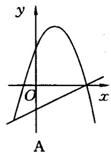
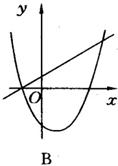
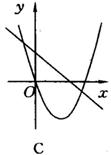
　　 分析:一次函数y=ax+c,当a>0时,图象过一、三象限;当a<0时,图象过二、四象限;c>0时,直线交y轴于正半轴;当c<0时,直线交y轴于负半轴;对于二次函数y=ax²+bx+c(a≠0)来讲:

　　 解:可用排除法,设当a>0时,二次函数y=ax²+bx+c的开口向上,而一次函数y=ax+c应过一、三象限,故排除C;当a<0时,用同样方法可排除A;c决定直线与y轴交点;也在抛物线中决定抛物线与y轴交点,本题中c相同则两函数图象在y轴上有相同的交点,故排除B.

　　 答案:D.

1. 二次函数解析式的确定

　　 例1 　求满足下列条件的二次函数的解析式

　　 (1)图象经过A(-1,3)、B(1,3)、C(2,6);

　　 (2)图象经过A(-1,0)、B(3,0),函数有最小值-8;

　　 (3)图象顶点坐标是(-1,9),与x轴两交点间的距离是6.

　 　分析:此题主要考查用待定系数法来确定二次函数解析式.可根据已知条件中的不同条件分别设出函数解析式,列出方程或方程组来求解.

　　 (1)解:设解析式为y=ax²+bx+c,把A(-1,3)、B(1,3)、C(2,6)各点代入上式得

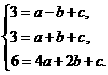　　　 　　　解得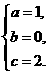

　　 ∴解析式为y=x²+2.

(2)解法1:由A(-1,0)、B(3,0)得抛物线对称轴为x=1,所以顶点为(1,-8).

设解析式为y=a(x-h)²+k,即y=a(x-1)²-8.

　　 把x=-1,y=0代入上式得0=a(-2)²-8,∴a=2.

　　 即解析式为y=2(x-1)²-8,即y=2x²-4x-6.

解法2:设解析式为y=a(x+1)(x-3),确定顶点为(1,-8)同上,

把x=1,y=-8代入上式得-8=a(1+1)(1-3).解得a=2,

∴解析式为y=2x²-4x-6.

　　 解法3:∵图象过A(-1,0),B(3,0)两点,可设解析式为:y=a(x+1)(x-3)=ax²-2ax-3a.

　　 ∵函数有最小值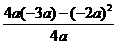-8.

　　 ∴=-8.

　　 又∵a≠0,∴a=2.

　　 ∴解析式为y=2(x+1)(x-3)=2x²-4x-6.

(3)解:由顶点坐标(-1,9)可知抛物线对称轴方程是x=-1,

又∵图象与x轴两交点的距离为6,即AB=6.

由抛物线的对称性可得A、B两点坐标分别为A(-4,0),B(2,0),

设出两根式y=a(x-x₁)·(x-x₂),

将A(-4,0),B(2,0)代入上式求得函数解析式为y=-x²-2x+8.

　 　点评:一般地,已知三个条件是抛物线上任意三点(或任意3对x,y的值)可设表达式为y=ax²+bx+c,组成三元一次方程组来求解;如果三个已知条件中有顶点坐标或对称轴或最值,可选用y=a(x-h)²+k来求解;若三个条件中已知抛物线与x轴两交点坐标,则一般设解析式为y=a(x-x₁)(x-x₂).

6.会构建二次函数模型解决一类与函数有关的应用性问题,应用数形结合思想来解决有关的综合性问题.