
题目列表(包括答案和解析)
23.(本题7分)A、桌面上放有4张卡片,正面分别标有数字1、2、3、4,这些卡片除数字外完全相同,把这些卡片反面朝上洗匀后放在桌面上,甲从中任意抽出一张,记下卡片上的数字后仍将反面朝上放回洗匀,乙从中任意抽出一张,记下卡片上的数字,然后将这两数相加.
(1)请用列表或画树状图的方法求两数和为5的概率.
(2)若甲与乙按上述方式作游戏,当两数之和为5时,甲胜;反之则乙胜.你认为这个游戏对双方公平吗?请说明理由;如果不公平,请你设计一个公平的规则,并说明理由.
B、小军与小玲共同发明了一种“字母棋”,进行比胜负的游戏.她们用四种字母做成10只棋子,其中A棋1只,B棋2只,C棋3只,D棋4只.
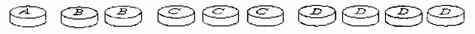
“字母棋”的游戏规则为:
①游戏时两人各摸一只棋进行比赛称一轮比赛,先摸者摸出的棋不放回;
②A棋胜B棋、C棋;B棋胜C棋、D棋;C棋胜D棋;D棋胜A棋;
③相同棋子不分胜负.
(1)若小玲先摸,问小玲摸到C棋的概率是多少?
(2)已知小玲先摸到了C棋,小军在剩余的9只棋中随机摸一只,问这一轮中小玲胜小军的概率是多少?
(3)已知小玲先摸一只棋,小军在剩余的9只棋中随机摸一只,问这一轮中小玲希望摸到哪种棋胜小军的概率最大?
22、已知:如图所示,BC为圆O的直径,A、F是半圆上异于B、C的一点,D是BC上的一点,BF交AH于点E ,A是弧BF的中点,AH⊥BC。
(1)求证:AE=BE(3分)
(2)如果BE·EF=32,AD=6,求DE、BD的长; (4分)

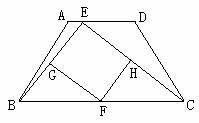
21.(本题6分)如图,等腰梯形ABCD中,AD∥BC,点E是线段AD上的一个动点(E与A、D不重合),G、F、H分别是BE、BC、CE的中点.
⑴试探索四边形EGFH的形状,并说明理由.(3分)
⑵当E运动到什么位置时,四边形EGFH是菱形?并加以证明.(3分)
20.已知关于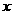 的一元二次方程
的一元二次方程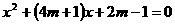 (本题6分)
(本题6分)
(1)求证:不论 为任何实数,方程总有两个不相等的实数根.
为任何实数,方程总有两个不相等的实数根.
(2)若方程两根为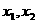 ,且满足
,且满足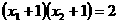 ,求
,求 的值.
的值.
19.(本题6分)解方程:(1)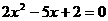
(2)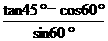 ·tan 30°+
·tan 30°+
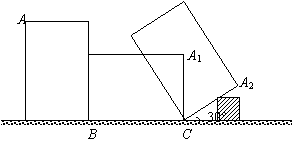
18、如图,王虎使一长为4 ,宽为 3
,宽为 3 的长方形木板,在桌面上做无滑动的翻滚(顺时针方向)木板上点A位置变化为
的长方形木板,在桌面上做无滑动的翻滚(顺时针方向)木板上点A位置变化为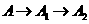 ,其中第二次翻滚被桌面上一小木块挡住,使木板与桌面成30°角,则点A翻滚到A2位置时共走过的路径长为
,其中第二次翻滚被桌面上一小木块挡住,使木板与桌面成30°角,则点A翻滚到A2位置时共走过的路径长为
17.如图,AB⊥BC,DC⊥BC,BC与以AD为直径的⊙O相切于点E,AB=9,CD=4,求四边形ABCD的面积

16. A如图,CD是Rt△ABC斜边上的高,AC=4,BC=3.
A如图,CD是Rt△ABC斜边上的高,AC=4,BC=3.
则cos∠BCD的值是
B、在ΔABC中,∠C=900,AD是角平分线, AC=24,AD=16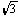 ,
,
则cos∠CAB=______。
15.△ABC是直径为10cm的圆内接等腰三角形,如果此三角形的底边BC=8cm,则△ABC的面积为___ _.
14.已知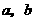 是一元二次方程
是一元二次方程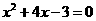 的两个实数根,则
的两个实数根,则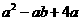 的值是______.
的值是______.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com