
题目列表(包括答案和解析)
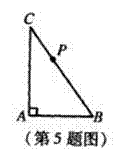
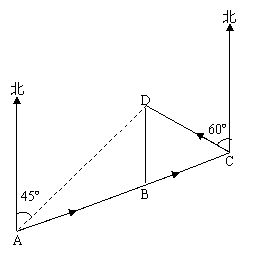
5.如图,P是Rt△ABC的斜边BC上 异于B、C的一点,过P点作
直线截△ABC,使截得的三角形与△ABC相似,满足这样条件的
直线共有( )条。
A.1 B.2
C.3 D.4
4.两个圆的半径分别是4cm和3cm,圆心距是7cm,则这两个圆的位置关系是 ( )
 A.外离 B.相交
A.外离 B.相交
C.内切 D.外切
3.在平面直角坐标系中,已知点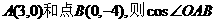 等于 ( )
等于 ( )
A.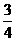 B.-
B.-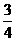 C.
C.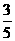 D.
D.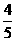
2.抛物线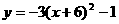 的对称轴是 ( )
的对称轴是 ( )
A. B.
B.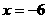 C.
C.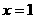 D.
D.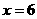
1.若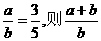 的值 ( )
的值 ( )
A.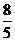 B.
B.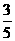 C.
C.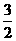 D.
D.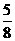
29.(本题9分)设抛物线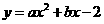 与x轴交于两个不同的点A(一1,0)、B(m,0),
与x轴交于两个不同的点A(一1,0)、B(m,0),
与y轴交于点C.且∠ACB=90°.
(1)求m的值和抛物线的解析式;
(2)已知点D(1,n )在抛物线上,过点A的直线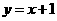 交抛物线于另一点E.若点P在x轴上,以点P、B、D为顶点的三角形与△AEB相似,求点P的坐标.
交抛物线于另一点E.若点P在x轴上,以点P、B、D为顶点的三角形与△AEB相似,求点P的坐标.
(3)在(2)的条件下,△BDP的外接圆半径等于________________.

28、(本题7分)
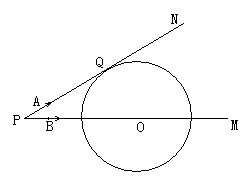 A、如图,已知⊙O的半径为6cm,射线PM经过点O,OP=10cm,射线PN与⊙O相切于点Q.A,B两点同时从点P出发,点A以4cm/s的速度沿射线PN方向运动,点B以5cm/s的速度沿射线PM方向运动. 设运动时间为
A、如图,已知⊙O的半径为6cm,射线PM经过点O,OP=10cm,射线PN与⊙O相切于点Q.A,B两点同时从点P出发,点A以4cm/s的速度沿射线PN方向运动,点B以5cm/s的速度沿射线PM方向运动. 设运动时间为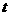 s.
s.
(1)求PQ的长;(4分)
(2)当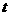 为何值时,直线AB与⊙O相切?(4分)
为何值时,直线AB与⊙O相切?(4分)
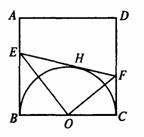
B、已知:如图,正方形ABCD的边长为2a,H是以BC为直径的半圆O上一点,过H与圆O相切的直线交AB于E,交CD于F.
(1)当点H在半圆上移动时,切线,EF在AB、CD上的两个交点也分别在AB、CD上移动(E、A不重合,F、D不重合),试问:四边形AEFD的周长是否也在变化?证观
你的结论;
(2)设△BOE的面积为S1,△COF的面积为S2,正方形ABCD的面积为S,且S1+S2
=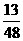 S,求BE与CF的长. (本题7分)
S,求BE与CF的长. (本题7分)
C、如图,BC是⊙O的直径,点A在圆上,且AB=AC=4.P为AB上一点,过P作PE⊥AB分别BC、OA于E、F
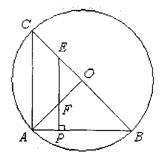 (1)设AP=1,求△OEF的面积.
(1)设AP=1,求△OEF的面积.
(2)设AP=a (0<a<2),△APF、△OEF的面积分别记为S1、S2。
①若S1=S2,求a的值;
②若S= S1+S2,是否存在一个实数a,使S<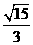 ?
?
若存在,求出一个a的值;若不存在,说明理由.
27、(本题7分)西瓜经营户以2元/千克的价格购进一批小型西瓜,以3元/千克的价格出售,每天可售出200千克.为了促销,该经营户决定降价销售.经调查发现,这种小型西瓜每降价O.1元/千克,每天可多售出40千克.另外,每天的房租等固定成本共24元.
(1)该经营户要想每天盈利2O0元,应将每千克小型西瓜的售价降低多少元?
(2)该经营户要想每天盈利最大,应将每千克小型西瓜的售价降低多少元?
25、(本题7分)已知二次函数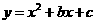 中,函数
中,函数 与自变量
与自变量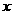 的部分对应值如下表:
的部分对应值如下表:
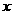 |
… |
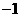 |
 |
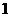 |
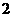 |
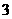 |
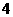 |
… |
 |
… |
 |
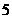 |
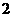 |
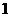 |
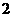 |
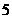 |
… |
(1)求该二次函数的关系式;
(2)当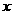 为何值时,
为何值时, 有最小值,最小值是多少?
有最小值,最小值是多少?
(3)若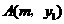 ,
,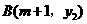 两点都在该函数的图象上,试比较
两点都在该函数的图象上,试比较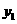 与
与 的大小.
的大小.
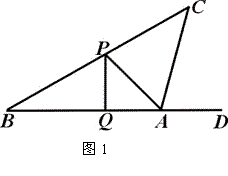
 26A、(本题7分)载着“点燃激情,传递梦想”的使用,6月2日奥运圣火在古城荆州传递,途经A、B、C、D四地.如图,其中A、B、C三地在同一直线上,D地在A地北偏东45º方向,在B地正北方向,在C地北偏西60º方向.C地在A地北偏东75º方向.B、D两地相距2km.问奥运圣火从A地传到D地的路程大约是多少?(最后结果保留整数,参考数据:
26A、(本题7分)载着“点燃激情,传递梦想”的使用,6月2日奥运圣火在古城荆州传递,途经A、B、C、D四地.如图,其中A、B、C三地在同一直线上,D地在A地北偏东45º方向,在B地正北方向,在C地北偏西60º方向.C地在A地北偏东75º方向.B、D两地相距2km.问奥运圣火从A地传到D地的路程大约是多少?(最后结果保留整数,参考数据: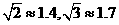 )
)
B、小唐同学正在操场上放风筝,风筝从A处起飞,几分钟后便飞达C处,此时,在AQ延长线上B处的小宋同学,发现自己的位置与风筝和旗杆PQ的顶点P在同一直线上.
(1)已知旗杆高为10米,若在B处测得旗杆顶点P的仰角为30°,A处测得点P的仰角为45°,试求A、B之间的距离;
(2)此时,在A处背向旗杆又测得风筝的仰角为75°,若绳子在空中视为一条线段,求绳子AC约为多少?(结果可保留根号)

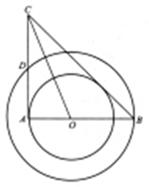
24、(本题7分)如图,在以O为圆心的两个同心圆中,AB经过圆心O,且与小圆相交于点A、与大圆相交于点B。小圆的切线AC与大圆相交于点D,且CO平分∠ACB。
(1)试判断BC所在直线与小圆的位置关系,并说明理由;
(2)试判断线段AC、AD、BC之间的数量关系,并说明理由;
(3)若AB=8㎝,BC=10㎝,求大圆与小圆围成的圆环的面积。(结果保留π)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com