
题目列表(包括答案和解析)
27、(本题8分)
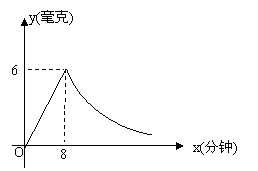
为了预防“传染病”,某学校对教室采用药薰消毒法进行消毒。已知药物燃烧时,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例,药物燃烧完后,y与x成反比例(如图所示),现测得药物8分钟燃毕,此时室内空气中每立方米的含药量为6毫克,请根据题中所提供的信息,解答下列问题:
(1)药物燃烧时y关于x的函数关系式为 ,自变量x的取值
范围是 ;药物燃烧后y关于x的函数关系式为 。
(2)研究表明,当空气中每立方米的含药量低于1.6 毫克时学生方可进教室,那么从消
毒开始,至少需要经过 分钟后,学生才能回到教室。
(3)研究表明,当空气中每立方米的含药量不低于3毫克且持续时间不低于10分钟时,
才能有效杀灭空气中的病菌,那么此次消毒是否有效?为什么?
26、(本题8分)
如图,Rt△AOB的顶点A(a,b)是一次函数
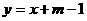 的图象与反比例函数
的图象与反比例函数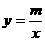 的
的
图象在第一象限内的交点,△AOB的面积为6,
求:(1)一次函数和反比例函数的解析式;
(2)点A的坐标
25、(本题6分)
某中学全体同学到距学校15千米的科技馆参观,一部分同学骑自行车先走,40分钟后,其余同学乘汽车出发,结果他们同时到达科技馆,已知汽车的速度是自行车速度的3倍,求汽车的速度。

24、(本题8分)
如图,在平行四边形ABCD中,过点B作BE⊥CD,垂足为E,连结AE,F为AE上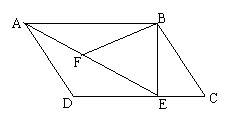 一点,且∠BFE=∠C,
一点,且∠BFE=∠C,
(1)求证:△ABF∽△EAD
(2)若AB=2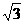 ,AD=3,BE=2,求BF的长
,AD=3,BE=2,求BF的长
23、(本题6分)
苏州市区某居民小区共有800户家庭,有关部门对该小区的自来水管网系统进行改造,
为此需了解该小区自来水用水情况,该部门通过随机抽取,调查了其中30户家庭,已知这30户家庭共有87人。
(1)这30户家庭平均每户 人(精确到0.1人);
(2)这30户家庭的月用水量见下表:
|
月用水量(m3) |
4 |
6 |
7 |
12 |
14 |
15 |
16 |
18 |
20 |
25 |
28 |
|
户数 |
1 |
2 |
3 |
3 |
2 |
5 |
3 |
4 |
4 |
2 |
1 |
求这30户家庭的人均日用水量(一个月按30天计算,精确到0.001 m3);
(3)根据上述数据,试估计该小区的日用水量(精确到1 m3)。
22、(本题6分)
如果一次函数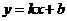 中自变量x的取值范围是
中自变量x的取值范围是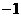 ≤
≤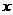 ≤3时,函数值y的取值范围是
≤3时,函数值y的取值范围是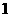 ≤
≤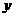 ≤3,求这个一次函数解析式。
≤3,求这个一次函数解析式。
21、解方程:((每小题4分,共8分)
(1)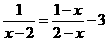 (2)
(2)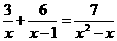
20、(每小题5分,共10分)
(1)先化简,再求值: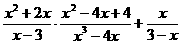 ,其中
,其中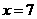
(2)有一道题:“先化简,再求值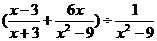 ,其中
,其中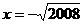 ”,小
”,小
亮同学做题时,把“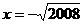 ”错抄成了“
”错抄成了“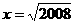 ”,但她的计算结果也
”,但她的计算结果也
是正确的,请你解释是怎么回事。
文字说明
19、(每小题4分,共8分)
(1)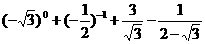 (2)
(2)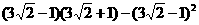
18、若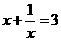 ,求
,求 的值是:
的值是:
(A)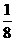 (B)
(B)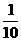 (C)
(C)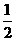 (D)
(D)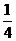
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com