26、(12分)某市种植某种绿色蔬菜，全部用来出口．为了扩大出口规模，该市决定对这种蔬菜的种植实行政府补贴，规定每种植一亩这种蔬菜一次性补贴菜农若干元．经调查，种植亩数y(亩)与补贴数额x(元)之间大致满足如图1所示的一次函数关系．随着补贴数额x的不断增大，出口量也不断增加，但每亩蔬菜的收益z(元)会相应降低，且z与x之间也大致满足如图2所示的一次函数关系．

(1)在政府未出台补贴措施前，该市种植这种蔬菜的总收益额为多少？

(2)分别求出政府补贴政策实施后，种植亩数y和每亩蔬菜的收益z与政府补贴数额x之间的函数关系式；

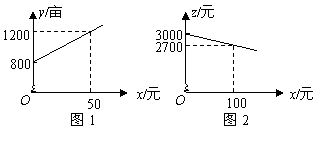(3)要使全市这种蔬菜的总收益w(元)最大，政府应将每亩补贴数额x定为多少？并求出总收益w的最大值．

25、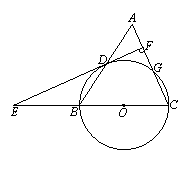(10分)如图，等腰三角形ABC中，AC＝BC＝10，AB＝12．以BC为直径作

⊙O交AB于点D，交AC于点G，DF⊥AC，垂足为F，交CB的延长线于点E．

(1)求证：直线EF是⊙O的切线；

(2)求sin∠E的值．

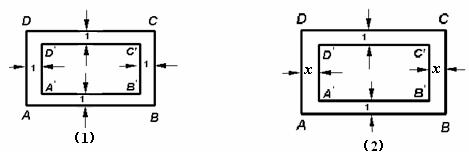
24、(10分)如图：矩形ABCD的长AB=30，宽BC=20．

(1)如图(1)若沿矩形ABCD四周有宽为1的环形区域，图中所形成的两个矩形ABCD与A′B′C′D′ 相似吗？请说明理由．

(2)如图(2)，x为多少时，图中的两个矩形ABCD与A′B′C′D′相似？

23、(10分)已知二次函数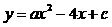的图像经过点A(－1 ，－1)和点B(3 ，－9)．

(1)求该二次函数的表达式；

(2)写出该抛物线的对称轴及顶点坐标；

(3)点P(m ，m)与点Q均在该函数图像上(其中m＞0)，且这两点关于抛物线的对称轴对称，求m的值及点Q 到y轴的距离．

22、(8分)“六一”儿童节前夕，我市某县“关心下一代工作委员会”决定对品学兼优的“留守儿童”进行表彰，某校八年级8个班中只能选两个班级参加这项活动，且8(1)班必须参加，另外再从其它班级中选一个班参加活动．8(5)班有学生建议采用如下的方法：将一个带着指针的圆形转盘分成面积相等的4个扇形，并在每个扇形上分别标上1，2，3，4四个数字，转动转盘两次，将两次指针所指的数字相加，(当指针指在某一条等分线上时视为无效，重新转动)和为几就选哪个班参加，你认为这种方法公平吗？请说明理由．

21、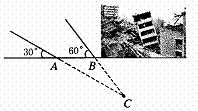(8分)某地震救援队探测出某建筑物废墟下方点 C 处有生命迹象，已知废墟一侧地面上两探测点A、B 相距 　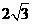米，探测线与地面的夹角分别是30°和 60°(如图)，试确定生命所在点 C 的深度．

20、(6分)如图，已知O是坐标原点，B、C两点的坐标分别为(3，－1)、(2，1)，

以O点为位似中心在y轴的左侧将△OBC放大到两倍(即新图与原图的相似比为2)．

(1)画出图形；

(2)分别写出B、C两点的对应点B′、C′ 的坐标；

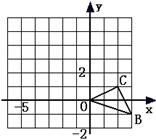(3)如果△OBC内部一点M的坐标为(x，y)，写出M位似变化的对应点M′ 的坐标．

19、(本题10分，每小题5分)

(1)计算：cos30°+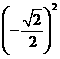－tan60°　 (2)解方程：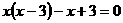

18、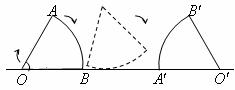如图，将半径为1、圆心角为60°的扇形纸片AOB，

在直线l上向右作无滑动的滚动至扇形A’O’B’处，则

顶点O经过的路线总长为　　　　　　 ．

17、已知⊙O₁与⊙O₂的圆心距为5，⊙O₁的半径为2，当⊙O₂的半径r满足条件

　　　　 　　　　时，两圆相离．