
题目列表(包括答案和解析)
4.根据与系数的关系,求与方程的根有关的代数式的值.
例4 (2004·河北)若x1,x2是一元二次方程2x2-3x+1=0的两个根,则x12+x22的值是( )
A. 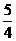 B.
B. 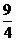 C.
C. 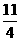 D.7
D.7
分析:本题解法不唯一,可先解方程求出两根,然后代入x12+x22,求得其值.但一般不解方程,只要将所求代数式转化成含有x1+x2和x1x2的代数式,再整体代入.
解:由根与系数关系可得x1+x2=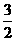 ,x1·x2=
,x1·x2=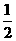 ,x12+x22=(x1+x2)2-2x1·x2=(
,x12+x22=(x1+x2)2-2x1·x2=(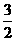 )2-2×
)2-2× 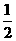 =
=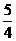 .
.
答案:A.
点评:公式之间的恒等变换要熟练掌握.
3. 解一元二次方程
例3 (2004·四川)解方程:x2+3x=10.
分析:根据方程的特点,可用公式法求解.
解:原方程就是x2+3x-10=0,
这里a=1,b=3,c=-10.
b2-4ac=32-4×1×(-10)=49.
∴x=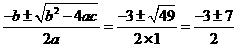 .
.
∴x1=2,x2=-5.
点评:要根据方程的特点灵活选用方法解方程.
2.由方程根的情况求字母系数的取值范围
例2 (2004·重庆)若关于x的一元二次方程x2+x-3m=0有两个不相等的实数根,则m的取值范围是( )
A.m>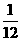 B.m<
B.m<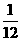 C.m>-
C.m>-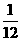 D.m<-
D.m<-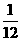
分析:因为该方程有两个不相等的实数根,所以应满足△>0.
解:由题意,得△=12-4×1×(-3m)>0,
解得 m>-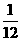 .
.
答案:C.
1.了解方程判定方程根的情况
例1 (2004·武汉)一元二次方程4x2+3x-2=0的根的情况是( ).
A.有两个相等的实数根; B.有两个不相等的实数根
C.只有一个实数根; D.没有实数根
解析:因为△=32-4×4×(-2)>0,所以该方程有两个不相等的实数根.
答案:B.
4.一元二次方程的应用
解应用题的关键是把握题意,找准等量关系,列出方程.最后还要注意求出的未知数的值,是否符合实际意义.
3.根与系数的关系(韦达定理)的应用
韦达定理:如果一元二次方程ax2+bx+c=0(a≠0)的两根为x1、x2,则x1+x2=-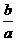 ,x1·x2=
,x1·x2=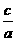 .
.
(1)已知一根求另一根及未知系数;
(2)求与方程的根有关的代数式的值;
(3)已知两根求作方程;
(4)已知两数的和与积,求这两个数;
(5)确定根的符号:(x1,x2是方程两根).
有两正根
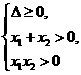
有两负根
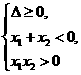
有一正根一负根
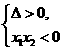
有一正根一零根

有一负根一零根
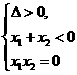
x1=x2=0
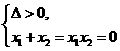
应用韦达定理时,要确保一元二次方程有根,即一定要判断根的判别式是否非负;求作一元二次方程时,一般把求作方程的二次项系数设为1,即以x1、x2为根的一元二次方程为x2-(x1+x2)x+x1x2=0;求字母系数的值时,需使二次项系数a≠0,同时满足△≥0;求代数式的值,常用整体思想,把所求代数式变形成为含有两根之和x1+x2,两根之积x1x2的代数式的形式,整体代入.
2.根的判别式及应用(△=b2-4ac)
(1)判定一元二次方程根的情况.
△>0 有两个不相等的实数根;
有两个不相等的实数根;
△=0 有两个相等的实数根;
有两个相等的实数根;
△<0 没有实数根;
没有实数根;
△≥0 有实数根.
有实数根.
(2)确定字母的值或取值范围.
应用根的判别式,其前提为二次系数不为0;考查时,经常和根与系数的关系、函数知识相联系、判别根的情况常用配方法.
1.灵活运用四种解法解一元二次方程
一元二次方程的一般形式:a2x+bx+c=0(a≠0)
四种解法:直接开平方法,配方法,公式法, 因式分解法,公式法:
x=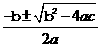 (b2-4ac≥0)
(b2-4ac≥0)
注意:掌握一元二次方程求根公式的推导;主要数学方法有:配方法,换元法,“消元”与“降次”.
┌───┬───────────┬────────────┐
│ │ │ 知识与技能目标 │
│ 考点 │ 课标要求 ├──┬──┬──┬───┤
│ │ │了解│理解│掌握│灵活应用
├───┼───────────┼──┼──┼──┼───┤
│ │了解一元二次方程的定义│ ∨ │ │ │ │
│ │及双重性 │ │ │ │ │
│ 一 ├───────────┼──┼──┼──┼───┤
│ 元 │掌握一元二次方程的四种│ │ │ │ │
│ 二 │解法,并能灵活运用 │ │ │ ∨ │ ∨ │
│ 次 ├───────────┼──┼──┼──┼───┤
│ 方 │掌握一元二次方程根的判│ │ ∨ │ ∨ │ ∨ │
│ 程 │别式,并能运用它解相应 │ │ │ │ │
│ │问题 │ │ │ │ │
│ ├───────────┼──┼──┼──┼───┤
│ │掌握一元二次方程根与系│ │ │ │ │
│ │数的关系,会用它们解决 │ │ ∨ │ ∨ │ ∨ │
│ │有关问题 │ │ │ │ │
│ ├───────────┼──┼──┼──┼───┤
│ │会解一元二次方程应用题│ │ │ ∨ │ │
└───┴───────────┴──┴──┴──┴───┘
23.解:解方程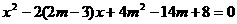 ,
,
得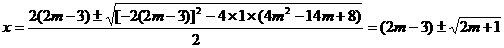 ,
,
∵原方程有两个不相等的整数根,∴2m+1为完全平方数,
又∵m为整数,且4<m<40,
∴m=12或24。
∴当m=12时,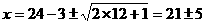 ,
,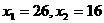 ;
;
当m=24时,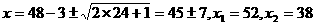
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com