
题目列表(包括答案和解析)
4.(2002·山西)有一种足球是由32块黑白相间的牛皮缝制而成的,如图所示,黑皮可看做正五边形,白皮可看做正六边形,设白皮有x块, 则黑皮有(32-x)块,每块白皮有六条边,共6x条边,因每块白皮有三条边和黑皮连在一起, 故黑皮共有3x条边,要求白皮、黑皮的块数,列出的方程正确的是( )
A.3x=32-x B.3x=5(32-x)
C.5x=3(32-x) D.6x=32-x
3.在公式P=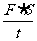 中,已知P、F、t都是正常数,则S等于(
)
中,已知P、F、t都是正常数,则S等于(
)
 A.
A.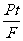 B.
B.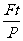 C.
C.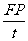 D.PFt
D.PFt
2.(2001·陕西)如果2(x+3)的值与3(1-x)的值互为相反数,那么x 等于( )
A.-8 B.8 C.-9 D.9
1.(2004·安徽)购某种三年期国债x元,到期后可得本息和y元,已知y=kx,则这种国债的年利率为( )
A.k B.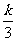 C.k-1 D.
C.k-1 D.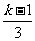
题型一 方程解的应用
例1(2004·芜湖)已知方程3x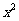 -9x+m=0的一个根是1,则m的值是 。 分析:根据方程解的定义,把方程的解x=1代入方程成立,然后解决关于m的方程即可,
-9x+m=0的一个根是1,则m的值是 。 分析:根据方程解的定义,把方程的解x=1代入方程成立,然后解决关于m的方程即可,
解:把x=1代入原方程,得3×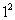 -9×1+m=0,
-9×1+m=0,
解得m=6
答案:6
点评:解题依据是方程解的定义,解题方法是把方程的解代入原方程,转化为关于待定系数的方程。
题型二 巧解一元一次方程
例2(2001·江苏)解方程: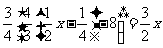
分析:此题先用分配律简化方程,再解就容易了。
解:去括号,得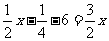
移项、合并同类项,得-x=6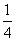 ,
,
系数化为1,得x=-6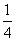
点评:解一元一次方程,掌握步骤,注意观察特点,寻找解题技巧,灵活运用分配委或分数基本性质等,使方程简化。
题型三 根据方程ax=b解的情况,求待定系数的值
例3已知关于x的方程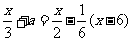 无解,则a的值是(
)
无解,则a的值是(
)
A.1 B.-1 C.±1 D.不等于1的数
分析:需先化成最简形式,再根据无解的条件,列出a的等式或不等式,从而求出a的值。
解:去分母,得2x+6a=3x-x+6,
即0·x=6-6a
因为原方程无解,所以有6-6a≠0,
即a≠1,
答案:D
题型四 一元一次方程的应用
例4(2004·福州)某班学生为希望工程共捐款131元,比每人平均2 元还多35元,设这个班的学生有x人,根据题意列方程为_________________。
解析:本题的相等关系是捐款总数相等,解决此题的关键是用学生人数、平均数与余数35元表示出捐款总数(2x+35)元。
答案:2x+35=131
基础达标验收卷
4.正确列一元一次方程解应用题
列方程解应用题,关键是寻找题中的等量关系,可采用图示、列表等方法,根据近几年的考试题目分析,要多关注社会热点,密切联系实际,多收集和处理信息,解应用题时还要注意检查结果是否符合实际意义。
3.理解方程ax=b在不同条件下解的各种情况,并能进行简单应用
方程ax=b:
(1)a≠0时,方程有唯一解x=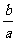 ;
;
(2)a=0,b=0时,方程有无数个解;
(3)a=0,b≠0时,方程无解。
2.正确理解方程解的定义,并能应用等式性质巧解考题
方程的解应理解为,把它代入原方程是适合的,其方法就是把方程的解代入原方程,使问题得到了转化。
1.会对方程进行适当的变形解一元一次方程
解方程的基本思想就是转化,即对方程进行变形,变形时要注意两点,一时方程两边不能乘以(或除以)含有未知数的整式,否则所得方程与原方程的解可能不同;二是去分母时,不要漏乘没有分母的项,一元一次方程是学习二元一次方程组、一元二次方程、一元一次不等式及函数问题的基本内容。
|
考点 |
课标要求 |
知识与技能目标 |
|||
|
了解 |
理解 |
掌握 |
灵活应用 |
||
|
一元一次方程 |
了解方程、一元一次方程以及方程有解的概念 |
∨ |
|
|
|
|
会解一元一次方程,并能灵活应用 |
∨ |
|
∨ |
∨ |
|
|
会列一元一次方程解应用题,并能根据问题的实际意义检验所得结
果是否合理。 |
|
∨ |
∨ |
∨ |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com