1．判断不等式是否成立

例1　 (2004·陕西)如图,若数轴的两点A、B表示的数分别为a、b,则下列结论正确的是(　 )

A.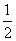b-a>0　　 B.a-b>0　　 C.2a+b>0　　 D.a+b>0

分析:首先由A、B两点在数轴上的位置分析出a、b的符号和绝对值的大小关系,再根据有理数法则进行选择.

解:由点A、B在数轴上的位置可知:

a<0,b>0,│a│>│b│.

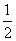∴ b>0,-a>0.

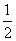∴ b-a>0.

故选A.

答案:A

4.列不等式(组)解应用题

注意分析题目中的不等量关系,考查的热点是与实际生活密切相联的不等式(组)应用题.

3.求不等式(组)的特殊解

不等式(组)的解往往是有无数多个,但其特殊解在某些范围内是有限的,如整数解、非负整数解,要求这些特殊解,首先是确定不等式(组)的解集, 然后再找到相应的答案.注意应用数形结合思想.

2.解一元一次不等式(组)

解一元一次不等式的步骤与解一元一次方程的步骤大致相同,应注意的是,不等式两边所乘以(或除以)的数的正负,并根据不同情况灵活运用其性质,不等式组解集的确定方法:若a<b,则有:

(1)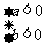 的解集是x<a,即“小小取小”.

(2) 的解集是x>b,即“大大取大”.

(3) 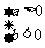的解集是a<x<b,即“大小小大取中间”.

(4)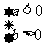 的解集是空集,即“大大小小取不了”.

一元一次不等式(组)常与分式、根式、一元二次方程、函数等知识相联系，解决综合性问题。

1.判断不等式是否成立

判断不等式是否成立,关键是分析判定不等号的变化,变化的依据是不等式的性质,特别注意的是,不等式两边都乘以(或除以)同一个负数时,要改变不等号方向;反之,若不等式的不等号方向发生改变,则说明不等式两边同乘以(或除以)了一个负数.因此,在判断不等式成立与否或由不等式变形求某些字母的范围时, 要认真观察不等式的形式与不等号方向.

6.(2004·陕西)足球比赛的记分规则为：胜一场得3分。平一场得1分，输一场得0分，一支足球队在某个赛季中共需比赛14场，现已比赛了8场，输了1场， 得17分，请问：

　　 (1)前8场比赛中，这支球队共胜了多少场？

　　 (2)这支球队打满14场比赛，最高能得多少分？

　　 (3)通过对比赛情况的分析，这支球队打满14场比赛，得分不低于29分， 就可以达到预期的目标，请你分析一下，在后面的6场比赛中， 这支球队至少要胜几场，才能达到预期目标？

5.(2001·江西)如图是某风景区的旅游路线示意图，其中B、C、D为风景点，E为两条路的交叉点，图中数据为相应两点间的路程(单位：km)一学生从A处出发，以2km/h的速度步行游览，每个景点的逗留时间均为0.5h。

　　 (1)当他沿着路线A-D-C-E-A游览回到A处时，共用了3h，求CE的长；

　　 (2)若此学生打自从A处出发后，步行速度与在景点的逗留时间保持不变，且在最短时间内看完三个景点返回到A外，请你为他设计一条步行路线，并说明这样设计的理由(不考虑其他因素)。

4.(2001·吉林)某初一学生在做作业时，不慎将墨水瓶打翻，使一道作业题只看到如下字样：“甲、乙两地相距40km，摩托车的速度为45km/h，运货汽车的速度为35km/h，_____________？”(横线部分表示被墨水覆盖的若干文字)请将这道作业题补充完整，并列方程解答。

3.(2004·柳州)一个一元一次方程的解为2，请你写出这个方程：______________。