
题目列表(包括答案和解析)
3.函数y=x2-2x+3的图象的顶点坐标是 ( )
A.(1,-4) B.(-1,2) C.(1,2) D.(0,3)
2.下列图形中既是中心对称图形又是轴对称图形的是 ( )

A B C D
1.抛物线y=(x-2)2+3的对称轴是 ( )
A.直线x=-3 B.直线x=3 C.直线x=-2 D.直线x=2

解:⑴ 如图:∵AB = BC = AC = 4  ,∴△ABC是正三角形。故∠C = 60°。
,∴△ABC是正三角形。故∠C = 60°。
当PQ⊥AC时,设BP = 1×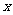 =
= ,则CQ = 2×
,则CQ = 2×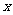 =2
=2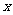 ,PC = 4 -
,PC = 4 - 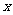
故 4 - 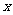 = 2×2
= 2×2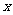 ,∴
,∴ 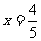 (
(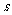 )
)
⑵ 如图:当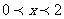 时,
时,
过Q作QE⊥BC于E,则QE = 2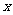 × sin60°=
× sin60°= 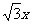 ,PD = 2 -
,PD = 2 -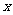
S△PQD = 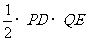
∴  (
(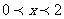 )
)
⑶
如图:当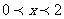 时,
时,
易知△POD-△PQE ,∴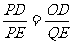
又易知 PD = DE
∴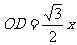
∴ S△POD
= 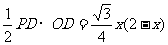

S△QOD = S△PQD
- S△POD = 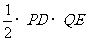 -
- 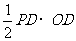
=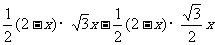
=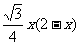
∴S△POD = S△QOD
本资料由《七彩教育网》 提供!
22.解:⑴依题意,得,月销售量为:500×(55-50)×10 = 450 (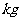 )
)
月销售利润为:450×(55-40)= 6750 (元)
⑵依题意,得,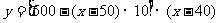 =
=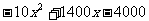
⑶依题意,得,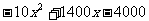 = 8000
= 8000
解之得,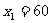
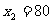
当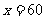 时,月销售量为400
时,月销售量为400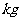 ,月销售成本为400×40 =16000元>10000元
,月销售成本为400×40 =16000元>10000元
当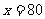 时,月销售量为200
时,月销售量为200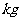 ,月销售成本为200×40 =8000元<10000元
,月销售成本为200×40 =8000元<10000元
因此销售单价应定为80元。
答:商店想在月销售成本不超过10000元的情况下,使得月销售利润达到8000元,销售单价应定为80元。
21. 解:如图,∵四边形PQMN是矩形,点Q、M在BC上,点P在AB上,点N在AC上
∴PN ∥ QM ∥ BC
又∵AD是高,


 ∴
∴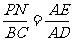 A
A
而ED = PQ
且PN︰PQ = 2︰1
故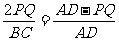


 ∴
∴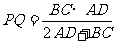 P
E
N
P
E
N

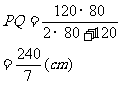 B Q
D
M C 四、应用题
B Q
D
M C 四、应用题
20. 证明:如图,∵AD是高,
∴∠ADB =90°
故△ABD是直角三角形
又∵E是AB的中点,
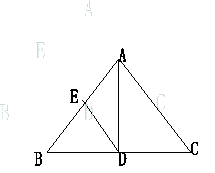

∴ DE
=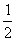 AB (直角三角形斜边上的中线等于斜边的一半. )
AB (直角三角形斜边上的中线等于斜边的一半. )
19.


18. 解:设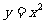 ,则原方程可化为
,则原方程可化为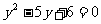
解得 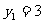
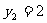
当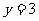 时,
时,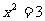 解得
解得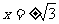 ,当
,当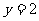 时,
时,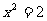 解得
解得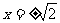
∴原方程的解为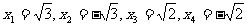
17. 原式= 2×1×sin220°+ 2sin270°
=2(sin220°+ cos220°)
=2×1
=2
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com