2．已知点P(2，-5)与点P′关于坐标原点对称，则点P′的坐标为　　　　　　 　。

1．如果x＝4是一元二次方程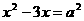的一个根，那么常数a的值是　　　　　 　。

23、(10分)解：，　 ，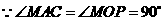

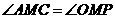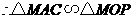．…………………… 2分

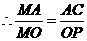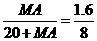，即．解得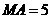．…………… 6分

同样由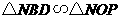可求得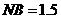．…………………… 8分

所以，小明的身影变短了3.5米．………………………………　 10分

24(10分)解： 过点C作CD⊥AB，交AB的延长线于D，设气球离地面的高度是x米，

在Rt△ACD中，∠CAD=45°，∴AD=CD=x.………………2分

在Rt△CBD中，∠CBD=60°，∴tan60°=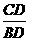,∴BD=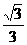x.……………6分

∵AB=AD-BD，即20=x-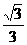x.　　 解得x=30+10.

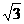即气球离地面的高度是(30+10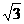)米。……………………10分

25(12分)解：(1)根据题意，得等腰梯形ABCD的周长为24，高为4，

面积为28.……………………1分

过点F作FG⊥BC于G，过点A作AK⊥BC于K，

则FG=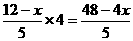，………………4分

所以S_△BEF=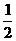BEFG=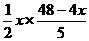=-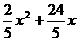(7≤x≤10).………………6分

(2)存在.……………………7分

由(1)得：-x²+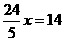，解得x₁=7,x₂=5(舍去).…………………10分

所以存在线段EF将等腰梯形ABCD的周长和面积同时等分，此时BE=7.…12分

26(12分)解：(1)∵DE∥BC,

∴△ADE∽△ABC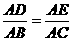，∴……………………2分

又∵AB=8,AC=6,DA=8-2x,AE=y,

∴

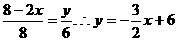
自变量的取值范围为0≤x≤4　 ………………………………6分

(2)

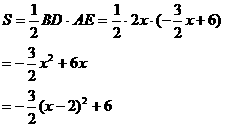………………………………9分

∴当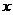=2时，S有最大值，且最大值为6. 　 ……………………12分

本资料由《七彩教育网》 提供！

22、(8分)解：(1)过点P作PA⊥x轴，垂足为A，

在Rt△OPA中，tanα= 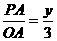，所以y=4.……………………4分

(2)设抛物线方程为y=a(x-3)²+4,

将(0，0)点代入得：a=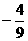

则所求方程为：y=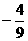 (x-3)²+4.…………………………8分

21、(8分)解：大双设计的游戏方案对双方不公平。…………1分

列举法或树状图说明理由(略)。………………………………4分

P(大双得到门票)=P(积为偶数)==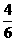

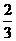
P(小双得到门票)=P(积为奇数)=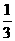…………………6分

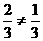∵　　 ∴大双设计的方案不公平。………………8分

16.1.28　　 17.7.24　　 18.120　　 19.不会　　 20.

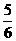
11. mcos40°　　 12.64 13.1　　 14.3或3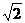　　　 15.　　　

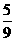
9、B　　 10、D　

1、C　　 2、B　　 3、C　　 4、C　　 5、A　　 6、B　　 7、A　　 8、A

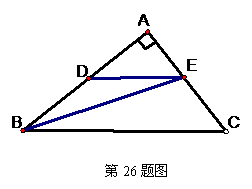
26．如图，在Rt△ABC中，∠A=90°,AB=8,AC=6.若动点D从点B出发，沿线段BA运动到点A为止，运动速度为每秒2个单位长度。过点D作DE∥BC交AC于点E,设动点D运动的时间为x秒，AE的长为y.

(1)求出y关于x的函数关系式，并写出自变量的取值范围；

(2)当x为何值时，△BDE的面积S有最大值，最大值为多少？

2008-2009学年度上学期期末教学评估

九年级数学答案及评分标准