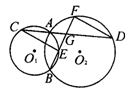
14．如图，已知⊙O₁与⊙O₂交于A，B两点，过A的直线交两圆于C，D两点，G为CD的中点，BG及其延长线交⊙O₁，⊙O₂于E，F，连结DF，CE，求证：CE=DF．

◆拓展训练

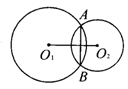
13．如图，已知⊙O₁与⊙O₂交于A，B，⊙O₁的半径为17，⊙O₂的半径为10，O₁O₂=21，求AB的长．

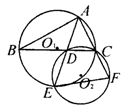
12．如图，△ABC中，∠BAC的平分线交BC于D，交△ABC的外接圆⊙O₁于E，过点C，D，E作⊙O₂，AC的延长线交⊙O₂于F．

　 (1)求证：EF²=ED·EA；

(2)若AE=6，EF=3，求AF·AC的值．

11．已知：AB为⊙O的直径，P为的中点，如图3－3－12所示．

　　 (1)若⊙O′与⊙O外切于点P(如图甲)，AP，BP的延长线分别交⊙O′于点C，D，连接CD，则△PCD是_______三角形；

　　 (2)若⊙O′与⊙O相交于点P，Q(如图乙)，连接AQ，BQ并延长分别交⊙O′于点E，F，请选择下列两个问题中的一个作答：

　　 问题一：判断△PEF的形状，并证明你的结论；

　　 问题二：判断线段AE与BF的关系，并证明你的结论．

我选择问题_______，结论：________．

10．已知两圆的半径分别是5和6，圆心距x满足不等式组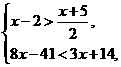，则两圆的位置关系是( )

　　 A．内切　　 B．外切　　 C．相交　　 D．外离

9．如图，PQ=3，以PQ为直径的圆与一个以5为半径的圆相切于点P，正方形ABCD的顶点A，B在大圆上，小圆在正方形的外部且与CD切于点Q，则AB=_______．

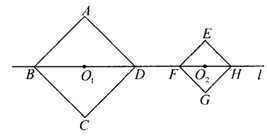
8．如图，正方形ABCD和正方形EFGH的边长分别为2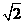和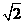，对角线BD，FH都在直线L上，O₁，O₂分别是正方形的中心，线段O₁O₂的长叫做两个正方形的中心矩．当中心O₂在直线L上平移时，正方形EFGH也随着平移，在平移时正方形EFGH的形状，大小没有改变．

　　 (1)计算：O₁D=_______，O₂F=_______．

　　 (2)当中心O₂在直线L上平移到两个正方形只有一个公共点时，中心距O₁O₂=_____．

(3)随着中心O₂在直线L上的平移，两个正方形的公共点的个数还有哪些变化？并求出相对应的中心距的值或取值范围(不必写出计算过程)．

◆提高训练

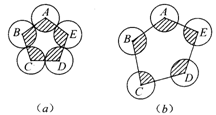
7．如图(a)所示，⊙A，⊙B，⊙C，⊙D，⊙E依次外切，半径都为1，依次连结五个圆心得五边形．

　 (1)求图(a)中五个扇形(阴影部分)的面积之和；

(2)求图(b)，若此五个圆相离，阴影部分的面积之和有变化吗？

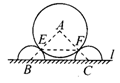
6．如图是某城市一个主题雕塑的平面示意图，它由置放于地面L上两个半径为2米的半圆与半径为4米的⊙A构成，点B，C分别是两个半圆的圆心，⊙A分别与两个半圆相切于点E，F，BC长为8米，求EF的长．

5．如图4，矩形ABCD中，AB=18，AD=25，去掉一个与三边相切的⊙M后，余下部分能剪出的最大圆的直径是(　 )

　　 A．8　　　　　 B．7　　　　 C．6　　　　 D．4