1.(2004·贵阳市)如图是一个正方体的平面展开图， 若在其中的三个正方形A、B、C内分别填上适当的数， 使得它们折成正方体后相对面上的两个数互为相反数，则填入正方形A、B、C内的三个数依次为(　　 )

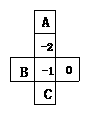　　 A.1，0，2　　 B.-1，0，-2　　 C.-2，0，-1　　 D.0，2，1

　　 题型一　 有关立体图形　

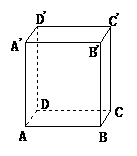　 　例1 　(2004·杭州市)在图所示的长方体中，和平面A1 C1 垂直的平面有(　　 )

　　 A.4个　　 B.3个　　　 C.2个　　　 D.1个

　　 解析：利用长方体的特征判断即可。

　　 答案：A。

　　 例2(2003·仙桃市)如图是一个正方体的展开图，每个图内都标注了字母，则展开与面E相对的是(　　 )

　　 A.面D　　 B.面B　　 C.面C　　 D.面A

　　 解析：已知这是一个正方体的表面展开图，共有6个面，其中和D相邻的有4 个面，它们是：A、C、F、B，因此和E相对的只有D。

　　 答案：A

　　 点评：为了培养空间的相象能力：一时要动手操作，仔细观察；二是要善于想象，把想象的样子亲自折一折，经过训练，就会大大提高自己的空间想象能力，另外，善于总结规律，会提高识别能力。

　　 题型二　 角的有关计算

　　 例3(2004·南京市)如查∠a=20°，那么∠a的补角等于(　　 )

　　 A.20°　　 B.70°　　 C.110°　　 D.160°

　 　解析：利用补角的定义，即可得出结果。

　　 答案：D

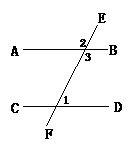
　　 例4(2003·长沙市)如图，AB∥CD，EF分别交AB、CD于点E、F，∠1=70°，则∠2=___________。

　 　解析：由AB∥CD可知∠1+∠3=180°。又因为∠2=∠3，所以∠1+∠2=180 °因此∠2=110°。

　　 答案：110°。

　　 题型三　 平行线的运用

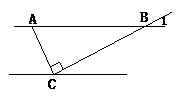　　 例5(2003·安徽)如图，已知：AB∥CD、AC⊥BC，图中与∠CAB 互余的角有(　 )

　　 A.1个　　 B.2个　　　 C.3个　　　 D.4个

　 　解析：由AC⊥BC，可知：∠CAB互余。又因为AB∥CD，所以∠ABC=∠BCD，又由对顶角的性质∠ABC=∠1。

　 　答案：C

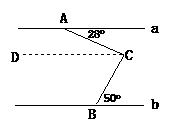　　 例6.(2004·贵阳市)如图，直线a∥b，则∠ACB=__________。

　　 解析：本题主要考查学生对问题的转化思想及分析、解决问题的能力，通过观察可作出过点C与a平行的直线，从而把问题化难为易。

　 　答案：78°

　　 点评：适当添加辅助线的解决几何问题的重要手段。

基础达标验收卷

3.平行线的性质与判定的运用

　　 平行线的特征与识别是互逆的，有时易混淆，在中考中往往综合运用，也经常与后续知识，平行四边形、相似形等相联系，是中考的重点之一。

2.角的有关计算

　　 这类问题一般主要考查互余、互补、对顶角的性质及平行线的性质的运用，首先根据已知条件观察图形，分析角与角之间的数量关系，从中找到解决问题的思路及途径，在中考中通常和三角形的内角和定理，内外角性质，或特殊三角形相联系。

1.立体图形的展开图

　　 这类问题，主要考查对立体图形与平面图形的关系的认识，因此要求掌握常用多面体的平面展开图的识别及逆向判断。

2．平面图形：点和线，两点之间线段最短。

　　 (1)角：对顶角相等，等角的补角相等，等角的余角相等；

　　 (2)平行线：两位角相等，两直线平行；两直线平行，同位角相等。

1．立体图形：视图，平面展开图；

16．设边长为2a的正方形的中心A在直线L上，它的一组对边垂直于直线L，半径为r的⊙O的圆心O在直线L上运动，点A，O间距离为d．

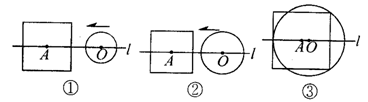
　　 (1)如图3－3－17①，当r<a时，根据d与a，r之间关系，将⊙O与正方形的公共点个数填入下表：

　　 所以，当r<a时，⊙O与正方形的公共点的个数可能有_______个．

　　 (2)如图3－3－17②，当r=a时，根据d与a，r之间关系，将⊙O与正方形的公共点个数填入下表：

　　 所以，当r=a时，⊙O与正方形的公共点个数可能有______个．

　　 (3)如图3－3－17③，当⊙O与正方形有5个公共点时，试说明r=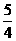a；

　　 (4)就r>a的情形，请你仿照“当……时，⊙O与正方形的公共点个数可能有_____个”的形式，至少给出一个关于“⊙O与正方形的公共点个数”的正确结论．

15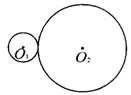．如图所示，已知⊙O₁与⊙O₂外切，它们的半径分别是1和3，那么半径为4且和⊙O₁，⊙O₂都相切的圆共有(　 )

A．1个　　　 B．2个　　 　C．5个　　　 D．6个