
题目列表(包括答案和解析)
2.有的时候认为n边形的外角和是一个变化的量,一定要记住无论是几边形,它的外角和总是等于360º的.
[基础演练]
1.在求n边形对角线的数目时,常认为有n(n-3)条,实际上过每个点有(n-3)条,n个点有n(n-3)条,但由于重复了一半,所以任意n边形有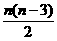 条对角线.
条对角线.
2.多边形的内角和与外角和的关系,如例3、例6.
[典例精析]
例1:任意n边形有( )条对角线. ( )
A.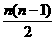 B.
B.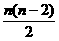 C.
C.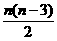 D.
D.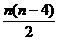
解析 由于过每个点可以作(n-3)条对角线,n个点有n(n-3)条,但由于每个点都重复了一次,所以任意n边形有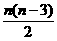 条对角线.故选答案C.
条对角线.故选答案C.
答案:C.
例2:若n边形恰好有n条对角线,则n为 ( )
A.4 B.5 C.6 D.7
解析 由于n边形有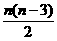 条对角线,所以
条对角线,所以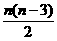 =n, 所以n=5. 故选答案B.
=n, 所以n=5. 故选答案B.
答案:B.
例3:若一个多边形的每一个内角都与它相邻的外角相等,则这个多边形是 ( )
A.三角形 B.正方形 C.五边形 D.不能确定
解析 由于多边形的每一个内角都与它相邻的外角的和是180°,假如每一个内角都与它相邻的外角相等,则内角和与它相邻的外角都是90°,则这个多边形是正方形.答案:B.
例4: 一个四边形最多可以有( )个钝角 ( )
A.一 B.两 C.三 D.四
解析 由于四边形的内角和都是360°,所以最多有3个钝角.
答案: C.
例5:某学生在计算四个多边形的内角和时,得到下列四个答案,其中错误的是( )
A.360° B.720° C.1960° D.180180°
解析 无论是几边形,内角和一定是180的整倍数.
答案: C.
例6:如果一个多边形的内角和是它的外角和的m倍,则这个多边形的边数是( )
A.m B.2m-2 C.2m D.2m+2
解析 由于内角和是(n-2)180 °,外角和是360°,所以(n-2)180 =360m,所以n=2m+2.
答案:D.
[常见误区]
1.n边形对角线的条数的数目,如例1、例2;
4.了解四边形的不稳定性及其作用.
3.理解多边形的内角和与外角和定理:
(1)几边形:平面内n(n≥3)条线段首尾顺次相接,如果其中任何两条线段都不在同一直线上,所组成的图形叫做n边形.
(2)多边形内角和定理:n边形内角和等于(n-2)·180°,(n≥3,n为自然数)
(3)多边形外角和定理:n边形外角和等于360°(n≥3,n为自然数)
2.掌握四边形的内角和等于360°,外角和等于360°的性质;
1.理解四边形与四边形的边、顶点、内角、对角线等概念;
四边形:平面内,四条线段首尾顺次相接,如果任何两条线段都不在同一直线上,所形成的图形叫做四边形;
边:组成四边形各边的线段; 顶点:相邻两边的公共点; 内角:从四边形内部看相邻两边所成的角,简称为角;对角线:连结四边形不相邻的两个顶点的线段;外角:四边形的一条边与相邻边延长线组成的角;
5.利用因式分解计算: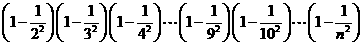 .
.
4.(2004·四川资阳)若非零实数a、b满足4a2+b2=4ab,则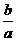 =_______.
=_______.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com