5． 若m是方程2x+1=3的一个解，则4m-5=　　　 。

4． 不等式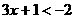的解集是　　　　 。

3． 2008年1月10日起,中国四川、贵州、湖南、湖北等19个省级行政区均受到低温、雨雪、冰冻灾害影响，直接经济损失537.9亿元,用科学记数法表示是　 　　　　　　元.

2． 回收废纸用于造纸可以节约木材．根据专家估计，每回收一吨废纸可以节约3立方米木材，那么回收吨废纸可以节约　　　 　立方米木材．

1．的绝对值是　　　　　 　.　　　　

23.(14分) 在学习扇形的面积公式,同学们得到扇形的面积公式,扇形有人也叫它“曲边三角形”,其面积公式类似于三角形的面积公式,把弧长看作底,把半径看作高就行了.当学了扇形的面积公式后,小明同学遇到这样一个问题:“某小区设计的花坛如下图中的阴影部分(扇环),它是一个大扇形去掉一个小扇形得到的,弧的长为弧的长为,求花坛的面积.”

受“曲边三角形”面积公式的启发,小明猜测扇环的面积应该类似梯形面积公式,他猜想花坛ABCD的面积,他的猜想对吗?如果正确,写出推导过程;如果不正确,请说明理由.

　　　　　　　　　　　　　　　　　　　　　　　　 　　　图14

2008-2009学年度学年度淮北市九年级“五校”联考

22.(12分) 已知：如图13,平面直角坐标系中,半圆的直径AB在x轴上,圆心为D.半圆交y轴于点C,AC=2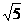,BC=4.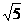

　(1)求以AO、BO两线段长为根的一个一元二次方程;

(2)求图象经过A、B、C三点的二次函数的表达式;

(3)设此抛物线的顶点为E,连接EC,试判断直线EC与⊙O的位置关系,并说明理由.

图13　　　

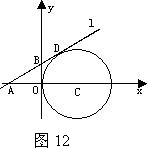
21.(12分) 如图12,在平面直角坐标系中,⊙C与y轴相切,且C点坐标为(1,0),直线过点A(-1,0),与⊙C相切于点D,求直线的解析式。

20.(10分) 赵州桥建于1400多年前的隋朝,是我国石拱桥中的代表性的桥梁,桥拱是圆弧形(如图11).经测量,桥拱下的水面距拱顶6 m时,水面宽34.64 m,已知桥拱跨度是37.4 m,运用你所学的知识计算出赵州桥的大致拱高.(注意：运算时取37.4=14,34.64=20)

　　　　　　　　　　　　　　　　　　　　　　　　　 图11

19.(10分) 如图10,CD,EF表示高度不同的两座建筑物,已知CD高15米,小明站在A处,视线越过CD,能看到它后面的建筑物的顶端E,此时小明的视角∠FAE=45°,为了能看到建筑物EF上点M的位置,小明延直线FA由点A移动到点N的位置,此时小明的视角∠FNM=30°,求AN之间的距离.