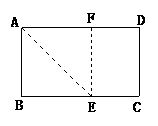
3.(2004.河南)如图3,一张矩形纸片,要折叠出一个最大的正方形, 小明把矩形的一个角沿折痕AE翻折上去,使AB和AD边上的AF重合,则四边形ABEF就是一个最大的正方形,他的判定方法是_________.

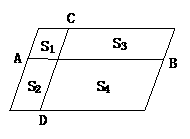
2.(2003,黄石)一个平行四边形被分成面积为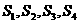的四个小平行四边形(如图2),当CD沿AB自左向右在平行四边形内平行滑动时,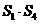与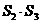的大小关系是______.

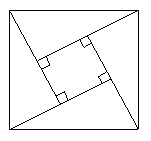
1.(2003.威海)2002年8月,在北京召开国际数学大会,大会会标是由4 个相同的直角三角形和1个小正方形拼成的大正方形(如图1),若大正方形的面积是34,小正方形的面积是4,则每个直角三角形的周长是______.

　　　　　 (1)　　　　　　　 (2)　　　　　　　　　　　　 (3)

4.(2003.徐州)有以下四个命题:

(1)两条对角线互相平分的四边形是平行四边形.

(2)两条对角线相等的四边形是菱形.

(3)两条对角线互相垂直的四边形是正方形.

(4)两条对角线相等且互相垂直的四边形是正方形,其中正确的个数为(　 )

A.8　　　 B.7　　　 C.6　　 D.5

3.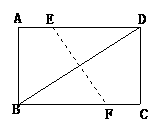(2003.恩施自治州)如图,在矩形ABCD中,AB=6,BC=8,若将矩形折叠, 使B点与D点重合,则折痕EF的长为(　 )

A.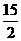　　　 B.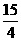　 　　C.5　　　 D.6

2.(2004.四川)下列说法中,错误的是(　 )

A.一组对边平行且相等的四边形是平行四边形

B.两条对角线互相垂直且平分的四边形是菱形

C.四个角都相等的四边形是矩形

D.邻边相等的四边形是正方形

1.(2003.苏州)如图,□ABCD中,∠C=108°,BE平分∠ABC,则∠ABE等于(　 )

A.18°　　 B.36°　　 C.72°　 D.108°

3．菱形的运用

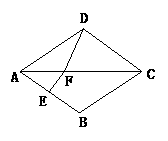
例3　 (2004.重庆)如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,E为垂足,连结DF,则∠CDF等于(　 )

A.80°　　 B.70°　　 C.65°　　 D.60°

解析:连结BF,由FE是AB的中垂线,知FB=FA,

于是∠FBA=∠FAB=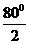=40°.

∴∠CFB=40°+40°=80°,

由菱形ABCD知,DC=CB.

∠DCF=∠BCF,CF=CF,于是△DCF≌△BCF,

因此∠CFD=∠CFB=°,

在△CDF中, ∠CDF=180°-40°-80°=60°.

答案:D.

点评:本题考查了线段中垂线的性质及菱形的特征,并借助全等解决问题, 平时应对重点知识注意积累.

基础达标验收卷

2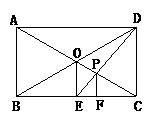．矩形的运用

例2　 (2004.广东深圳市)如图,在矩形ABCD中,对角线AC、BD相交于点O, 连O点作OE⊥BC于E,连结DE交AC于点P,过P作PF⊥BC于F,则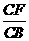的值是_________.

解析:利用矩形性质及平行线分线段成比例定理可得出结论.

答案:。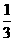

1．平行四边形的运用

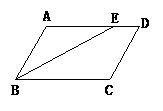
例1 　(2004.重庆万州区)如图,∠1=∠2,则下列结论一定成立的是(　 )

A.AB∥CD　 B.AD∥BC　　 C.∠B=∠D　　 D.∠3=∠4

解析:由平行线的识别知∠1=∠2,则AD∥BC.

答案:B.