
题目列表(包括答案和解析)
6.(2003·山东泰安)一种商品进价为每件a元,按进价增加25%出售, 后因库存积压降价,按售价的九折出售,每件还盈利( )
A.0.125a元 B.0.15a元 C.0.25a元 D.1.25a元
5.(2003·海南)某专卖店在统计2003年第一季度的销售额时发现,二人份比一月份增加10%,三月份比二月份减少10%,那么三月份比一月份( )
A.减少10% B.增加10% C.不增不减 D.减少1%
4.(2003·山西)某药店经营的抗病毒药品,在市场紧缺的情况下提价100 %,物价部门查处后,限定其提价的幅度只能是原价的10%,则该药品现在降价的幅度是( )
A.45% B.50% C.90% D.95%
3.(2003·四川省)当代数式a+b的值为3时,代数式2a+2b+1的值是( )
A.5 B.6 C.7 D.8
2.(2003·宁夏)当x=-2时,代数式-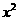 +2x-1的值等于(
)
+2x-1的值等于(
)
A.9 B.6 C.1 D.-1
1.(2003·北京石景山)a,b两数的平方和用代数式表示为( )
A.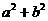 B.
B.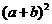 C.
C.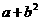 D.
D.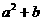
3.公式的探求与应用
探求公式时要先观察其中的规律,通过尝试,归纳出公式,再加以验证,这几个环节都是必不可少的,再就是灵活运用公式解决实际问题。
中考题型例析
题型一 代数式识别
例1 判别下列各式哪些是代数式,哪些不是代数式。
(1)a2-ab+b2;(2)S=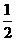 (a+b)h;(3)2a+3b≥0;(4)y;(5)0;(6)c=2
(a+b)h;(3)2a+3b≥0;(4)y;(5)0;(6)c=2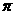 R。
R。
分析:这是考查代数式概念的题目,代数式的意义一定要明确.
答案:(1)(4)(5)都是代数式;(2)(3)(6)不是代数式。
点评:代数式区别于公式和等式,公式和等式含“=”而代数式不含“=”,也不同于不等式。
题型二 列代数式
例2 (2003·黑龙江哈尔滨)抗“非典”期间,个别商贩将原来每桶价格a元的过氧乙酸消毒液提价20%后出售,市政府及时采取措施,使每桶的价格在涨价一下降15%,那么现在每桶的价格是_____________元。
分析:本题是以抗“非典”期间清毒液销售价格的波动为素材而设置的一道列代数式的问题,要求考生抓住题目中的升降关键词,将题中的数量关系用代数式来表示,即有
a(1+20%)(1-15%)=1.02a(元)。
答案:1.02a。
题型三 探求公式
例3 (2002·北京)观察下列顺序排列的等式:
9×0=+1=1,9×1+2=11,9×2+3=21,9×3+4=31,9×4+5=41,...
猜想第n个等式,(n为正整数)应为 。
分析:从左边看,规律为第一项都是9;第二项分别为0,1,2,3,4,..., 第三项比第二项依次多1,即为1,2,3,4,5,...,从右边看,各项依次多10。 因此若设项数为n个等式应为9×(n-1)+n=1+(n-1)×10。
答案:9×(n-1)+n=10n-9。
基础达标验收卷
2.迅速求代数式的值
求代数式的值通常要先化简再求值比较简便,当所代的数是负数时,要特别注意符号。
1.正确列代数式
首先要注意审题,弄清问题中的基本数量关系,然后把数量关系用代数式表示出来,再就是要把代数式和等式区分开,书写代数式要注意格式。
|
考点 |
课标要求 |
知识与技能目标 |
|||
|
了解 |
理解 |
掌握 |
灵活应用 |
||
|
代 数 式 |
定义 |
∨ |
|
|
|
|
会列代数式 |
|
∨ |
∨ |
|
|
|
会求代数式的值 |
|
∨ |
∨ |
|
|
|
会归纳公式、应用公式 |
|
|
|
∨ |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com