1.平面直角坐标系的有关概念

平面直角坐标系的有关概念不要死记硬背,应紧密结合坐标系来认识;在坐标平面内会正确地描点,对于坐标平面内的点要借助图形正确地写出,特别注意各象限内点的坐标符号.

2. 函数: 函数概念, 函数自变量取值范围, 函数的表示法(解析法,列表法,图象法), 函数的图象.

1.平面直角坐标系:平面直角坐标系概念, 坐标平面内点的坐标特征, 不同位置点的坐标特征.

5．　 检验不等式或不等式组的解集是否合理或是否符合实际情况，再写出答句.

为了说明上述五个步骤和不等式在实际生活中的应用，现列举几例加以说明.

例1．若干人乘坐若干辆汽车，如果每辆汽车坐22人，有1人不能上车；如果有一辆车放空，那么所有旅客正好能平均分乘到其它各车上.已知每辆车最多能容纳32人，求汽车数和旅客数.

解：设原有k辆汽车，开走一辆空车后平均每辆乘坐n名旅客，由题意得:

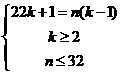
由①，得n=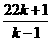==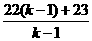22 + .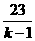

因为n是自然数，所以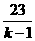必须是整数，

又23是质数，所以k - 1 =1或k -1=23，即k=2或k=24.

当k=2时，n = 45 > 32不合题意，舍去；当k=24时，n=23,符合问题要求，此时旅客人数为：n(k-1)=23×23=529(人).

答：汽车为24辆，旅客有529人.

例2．(2003年哈尔滨)慧秀中学在防“非典”知识竞赛中，评出一等奖4人，二等奖6人，三等奖20人，学校决定给所有获奖学生各发一份奖品，同一等次的奖品相同．

(1)若一等奖，二等奖、三等奖的奖品分别是喷壶、口罩和温度计，购买这三种奖品共计花费113元，其中购买喷壶的总钱数比购买口罩的总钱数多9元，而口罩的单价比温度计的单价多2元，求喷壶、口罩和温度计的单价各是多少元？

(2)若三种奖品的单价都是整数，且要求一等奖的单价是二等奖单价的2倍，二等奖的单价是三等奖单价的2倍，在总费用不少于90元而不足150元的前提下，购买一、二、三等奖奖品时它们的单价有几种情况，分别求出每种情况中一、二、三等奖奖品的单价？

解：(1)设喷壶和口罩的单价分别是y元和z元，根据题意，得

, 解得, 所以，z - 2=2.5.

因此，喷壶、口罩和温度计的单价分别是9元、4.5元和2.5元.

(2)设三等奖奖品的单价为x元，则二等奖奖品的单价为2x元，一等奖奖品的单价为4x元. 根据题意，得

90≤4×4x+6×2x+20x<150，解得1≤x<3.

因为三种奖品的单价都是整数，所以x=2，或者x=3.

当x=2时，2x=4, 4x=8；当x=3时，2x=6, 4x=12.

因此，购买一、二、三等奖奖品时它们的单价有两种情况，第一种情况中一、二、三等奖奖品的单价分别是8元、4元和2元；第二种情况中一、二、三等奖奖品的单价分别是12元、6元和3元.

例3．(2006年黑龙江)为了保护环境，某企业决定购买10台污水处理设备，现有A、B两种型号的设备，其中每台的价格、月处理污水量及年消耗费如下表：

经预算，该企业购买设备的资金不高于105万元.

(1)请你设计该企业有几种购买方案；

(2)若企业每月产生的污水量为2040吨，为了节约资金，应选择哪种购买方案；

(3)在第(2)问的条件下，若每台设备的使用年限为10年，污水厂处理污水费为每吨10元，请你计算，该企业自己处理污水与将污水排到污水厂处理相比较，10年节约资金多少万元？(注：企业处理污水的费用包括购买设备的资金和消耗费)

分析：(1)设购买污水处理设备A型x台，则B型(10 – x)台，由题意知：

12x+10(10 – x)≤105，解得x≤2.5

因为x是非负整数，所以x可取0、1、2

因此有三种购买方案：①购A型0台，B型10台；②购A型1台，B型9台；③购A型2台，B型8台.

(2)同(1)所设，可以列出以下不等式.

240x+200(10 – x )≥2040，解得x≥1，所以x为1或2

当x＝1时，购买资金为：12×1+10×9＝102(万元)

当x＝2时，购买资金为：12×2+10×8＝104(万元)

因此为了节约资金，应选购A型1台，B型9台.

(3)10年企业自己处理污水的总资金为：102+10×10＝202(万元)

若将污水排到污水厂处理，10年所需费用为：

2040×12×10×10＝2448000(元)＝244.8(万元)

因为244.8－202＝42.8(万元)

所以能节约资金42.8万元.

例4.(2006山东枣庄)现计划把甲种货物1240吨和乙种货物880吨用一列货车运往某地，已知这列货车挂有A、B两种不同规格的货车厢共40节，使用A型车厢每节费用为6000元，使用B型车厢每节费用为8000元．

(1)略；

(2)如果每节A型车厢最多可装甲种货物35吨和乙种货物15吨，每节B型车厢最多可装甲种货物25吨和乙种货物35吨，装货时按此要求安排A、B两种车厢的节数，那么共有哪几种安排车厢的方案？

(3)在上述方案中，哪个方案运费最省？最少运费为多少元？

分析：(2)设用A型车厢x节，则用B型车厢(40－x)节，依题意，得

，解得 24≤x≤26．　　　　　　　　　　　　　　　　　　　　

因为x取整数，故A型车厢可用24节或25节或26节．相应有三种装车方案：

①24节A型车厢和16节B型车厢；②25节A型车厢和15节B型车厢；③26节A型车厢和14节B型车厢．

(3)方案①中，运费为6000×24+8000×16=144000+128000=272000(元)；

方案②中，运费为6000×25+8000×15=150000+120000=270000(元)；

方案③中，运费为6000×26+8000×14=156000+112000=268000(元).

因为268000<270000<272000，

所以按照方案③，安排A型车厢26节、B型车厢14节运费最省．最小运费为26.8万元．

4．　 解这个不等式或不等式组，求出不等式或不等式组的解集；

3．　 根据这些不等的关系列出所需的代数式，从而列出不等式或不等式组；

2．　 找出能够表示应用题全部含义的一个或几个不相等的关系；

1．　 读懂题意和题目中的数量关系，用字母(如)表示题目中的一个未知数；

4.(2003·北京宣武区)按下列程序计算，把答案填在表格内，然后看看有什么规律，想想为什么会有这个规律？

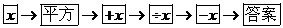
　　 (1)填写表内空格：

输入x	3	2	-2		...
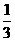输出答案	1	1			...

　　 (2)发现的规律是：____________________。

　　 (3)用简要的过程证明你发现的规律。