5.实际问题中函数解析式的求法

例7 　(2003·新疆)乌鲁木齐至库尔勒的铁路长约600km,火车从乌鲁木齐出发, 其平均速度为58km/h,则火车离库尔勒的距离s(km)与行驶时间t(h)的函数关系式是________.

解析:已知s表示火车离库尔勒的距离,t表示火车从乌鲁木齐出发行驶的时间, 火车速度已知,所以s=总路程-火车从乌鲁木齐出发行驶的路程.

答案:s=600-58t.

点评:此题主要考查实际问题中函数解析式的求法.理解题意, 弄清题目中数量关系是解题的关键.

达标练习

4. 函数图象

例6 　(2003·四川)小明骑自行车上学,开始以正常速度匀速行驶,但行至中途自行车出了故障,只好停下来修车.车修好后,因怕耽误上课,他比修车前加快骑车速度继续匀速行驶,下面是行驶路程s(m)关于时间t(min)的函数图象,那么符合这个同学行驶情况的图象大致是(　 ).

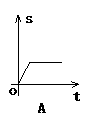
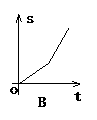
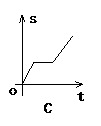
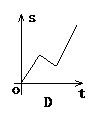
解析:A表示小明一直在停下来修车,而没继续向前走,B表示没有停下来修车,相反速度骑的比原来更快,D表示修车时又向回走了一段路才修好后又加快速度去学校.选项C符合题意.

答案:C.

点评:会看图象中横纵坐标表示的实际意义是解题的关键,此题主要考查函数知识及数形结合的数学思想.

3.自变量取值范围

例5 　(2003·南通)函数y=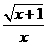中自变量x的取值范围是(　 )

A.x≥-1　　 B.x>0　　 C.x>-1且x≠0　　 D.x≥-1且x≠0

解析:要使y=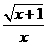有意义,需既使分式有意义,又使偶次根式有意义,即x≠0且x+1≥0,得x≥-1且x≠0.

答案:D.

点评:考查自变量取值范围是历年中考热点,本题中既要使根式有意义又要使分式有意义,需两者都考虑.

2.不同位置点的坐标特征

例3 　(2003·辽宁)在平面直角坐标系中,点P(-1,1)关于x轴的对称点在(　 ).

A.第一象限　　 B.第二象限　　 C.第三象限　　 D.第四象限

解析:点P(-1,1)关于x轴对称点的横坐标不变,纵坐标相反,∴P(-1,1)关于x 轴的对称点坐标为(-1,-1)在第三象限.

答案:C.

点评:关于x轴对称点的横坐标相等,纵坐标互为相反数;关于y 轴对称点的纵坐标相等,横坐标互为相反数;关于原点对称点的横、纵坐标都互为相反数.

例4 　(2003·潍城)已知点A(m,-2),点B(3,m-1),且直线AB∥x轴,则m值为____.

解析:根据平行于x轴的直线上所有点的纵坐标相同,可得m-1=-2,可得m=-1.

答案:-1.

点评:平行于x轴的直线上所有点的纵坐标相同,平行于y轴的直线上所有点的横坐标相同.

1．坐标平面内点的坐标特征

例1　 (2003·潍坊)如果点M(a+b,ab)在第二象限,那么点N(a,b)在第____象限.

解析:由M在第二象限,可知a+b<0,ab>0可确定a<0,b<0,从而确定N在第三象限.

答案:三.

点评:本题主要考查各象限内点的坐标特征,即点P(x,y)在第一象限x>0,y>0; 点P(x,y)在第二象限x<0,y>0;点P(x,y)在第三象限x<0,y<0;点P(x,y)在第四象限x>0,y<0.

例2 　(2004.广州)点P在第二象限,若该点到x轴的距离为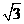,到y轴的距离为1,则点P的坐标是(　 )

A.(-1,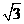)　　 B.(-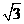,1)　　 C.(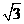,-1)　　 D.(1,)

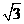解析:点P(x,y)到x轴的距离是│y│,到y轴的距离是│x│,且P在第二象限知x<0,y>0,可确定点P的坐标.

答案:A.

6.函数的图象

描点法画函数图象的三个步骤:列表、描点、连线，选取点时,尽量选取有代表性的合理的点,连线时,应用光滑的曲线连结.

对观察实际问题的图象,要正确理解横纵坐标表示的意义.

5.自变量取值范围

自变量的取值范围首先要考虑自变量所在代数式是分式还是偶次根式还要整式,然后从自变量取值必须使解析式有意义等方面来求解,注意实际问题要实际对待.

4.函数概念

对于函数的概念要正确地理解两个变量的关系.

3.不同位置点的坐标特征

对于平行于两坐标轴的直线上点的坐标特点应借助于平面直角坐标系来应用.

对于对称点的坐标特征应遵循:关于x轴对称的两点,横坐标不变,纵坐标相反; 关于y轴对称的两点,横坐标相反,纵坐标不变;关于原点对称的两点, 横纵坐标都互为相反数,或借助图形来完成,切忌死背.

注意P(x,y)到两坐标轴的距离与线段长度的区分.

2.坐标平面内点的坐标特征

注意两坐标轴上点的坐标的不同,且x轴、y轴不属于任何一个象限.