4.(2004.河北)如图3,在梯形ABCD中,AD∥BC,对角线AC⊥BD,且AC=12,BD=9,则此梯形的中位线长是(　 )

A.10　　　 B.　　　 C.　　　 D.12

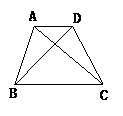
3.(2003.仙桃市、潜江市、江汉油田)如图2,线段AC、BD相交于点O,欲使四边形ABCD成为等腰梯形,满足的条件是(　 )

A.AO=CO,BO=DO　　　　　　　 B.AO=CO,BO=DO,∠ACB=90°

C.AO=DO,BO=CO,且AO≠CO　　 D.AO=DO,∠AOD=90°

2.(2003.南通)梯形的上底长为a,下底长是上底长的3倍,则梯形的中位线长(　　 )

A.4a　　 B.2a　　 C.1.5a　　 D.a

1.(2002.荆州)如图1,在梯形ABCD中,AB∥CD,∠D=2∠B,AD=a,CD=b, 则AB等于(　 )

A.a+　　 B.+b　　 C.a+b　　 D.a+2b

　　　 (1)　　　　　　　 (2)　　　　　　　 (3)　　　　　　　　 (4)

3. 梯形知识的综合运用

例3　 (2004.上海)如图,等腰梯形ABCD中,AD∥BC,∠DBC=45°,翻折梯形ABCD,使点B重合于D,折痕分别交边AB、BC于点F、E,若AD=2,BC=8.

求:(1)BE的长;(2)∠CDE的正切值.

分析:本题运用轴对称及等腰梯形的性质可解决.

解:(1)由题意得△BEF≌△DFE,

∴DE=BE,∵在△BDE中,DE=BE,∠DBE=45°,

∴∠BDE=∠DBE=45°,∴∠DEB=90°,

∴DE⊥BC.

∴EC=(BC-AD)= (8-2)=3.

∴BE=5.

(2)由(1)得DE=BE=5,在△DEC中,∠DEC=90°,DE=5,EC=3,

∴tan∠CDE=.

点评:本题是一道综合题目,它把梯形、全等、三角函数等知识综合在一起，考查了综合运用知识的能力。

基础达标验收卷

2.等腰梯形的有关计算

例2 　(2003.潍坊)已知:如图,等腰梯形ABCD中,AD∥BC,AD=3,AB=4, BC=7.求∠B的度数.

解:如过A点作AE∥CD,有 □AECD,则△ABE为等边三角形.

答案:∠B=60°.

点评:在梯形中常通过作腰的平行线,构造平行四边形、三角形, 从而把分散的条件集中到三角形中去,从而为证题创造必要的条件.

1．梯形的运用

例1 　(2003.潍坊)如图,在梯形ABCD中,已知AB∥CD,点E为BC的中点, 设△DEA的面积为,梯形ABCD的面积为,则与的关系为_______.

分析:由E点为BC的中点,故可联想延长DE与AB的延长线相交,将梯形的面积转化成三角形的面积.

答案:.

点评:将四边形转化成三角形是寻求解题思路,探求解题方法的重要途径, 注意适当地作出辅助线,学会转化的数学思想.

2.三角形、梯形中位线的应用

①注意三角形的中位线与三角形的中线的区别.

②在实际问题中常过一边的中点作另一边的平行线从而运用中位线定理解决问题.

1.梯形的运用

有关梯形问题, 常常用添加辅助线的方法把梯形转化成特殊四边形与三角形的问题来解决.如:作高、平移一腰、平移对角线、延长两腰交于一点、过一腰中点作另一腰的平行线等.