1、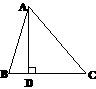求线段长度：利用勾股定理建立方程(即：方程思想)求解。

例1．在△ABC中，AB=13，BC=14，AC=15，求点A到BC边的距离。

6．在袋中装有大小、形状、质量完全相同的3只白球和3个红球, 两人从中进行摸球游戏,在游戏之前两人就各有10分,然后从中轮番摸球,每次摸三个球,然后放回袋中搅匀由另一个人摸球,记分规则如下:

　　 最后以得分高者为胜者.

　　 请问这个游戏对甲、乙双方公平吗?如果不公平,谁更合算?如果公平,则说明理由.

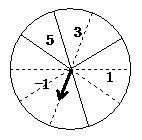
5．下面是一个可以自由转动的转盘,用这个转盘进行转盘游戏,转动转盘, 当它停止转动时,指针对准哪个区域,则将获得该区域上所有数字的分数,在玩游戏前,预测一下转很多次以后,游戏者平均每次将获得多少分?然后找一个伙伴, 尽可能多地做实验,由此检验你的预测.

4.在第3题的游戏中,小亮第1次抽到一张“大王”,得到10分,而小雅第1次抽到一张红桃,得到2分,于是小亮说:“我现在不抽了,你继续抽,到满50次后, 我俩再比例,谁的得分多谁赢”,你认为这对于小雅来说,合算吗?

3.小雅与小亮用一副扑克牌玩游戏,并约定:将牌洗匀后, 每次从中任取一张牌,然后放回再洗匀,两人轮番抽牌,如果抽出的牌是“大王”,则奖10分, 抽出“小王”则奖5分,抽出红桃则奖2分,抽出方块不奖分,抽出黑桃或梅花时,则罚2分,抽50次后,以所得分数的多少定输赢.

　　 (1)求每一次抽牌所获得的分数的平均数.

　　 (2)小亮抽50次后,得分为5分,于是他认为上述计算结果有问题, 你同意小亮的意见吗?为什么?

2.小明认为转盘不易操作,于是他用20只除颜色外都相同的小球,进行摸球游戏,这20只球中有1只红球,2只黄球,4只绿球,13只白球,每次从中摸出1球,并规定:摸到红球可获得100元购物券,摸到黄球可获得50元购物券,摸到绿球可获得20 元购物券,摸到白球则不能获购物券,求每次摸球所获购物券的平均数, 并与课本中的转盘实验中的结果相比较,说明其中的原因.

1.　　　 在一次转盘游戏中,小文根据实验数据绘制出下面的扇形统计图,求每转动一次转盘所获购物券金额的平均数.

4.2 哪种方式更合算 同步练习

25.(1)当t=2时，(如图1)，Q与D重合，P恰好是AB的中点， ，

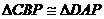则PQ=CP

(2)当2<t≤4时，(如图2)Q在CD上，过Q作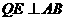于E，AE=QD=2t-4，AP=t.PE=t-(2t-4)=4-t.PB=4-t，PB=PE,BC=EQ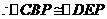，PC=PQ仍然成立

(3)当0≤t≤2时，(如图3)，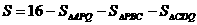

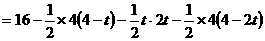
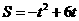
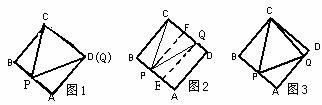
当2<t≤4时，QD=2t-4，CQ=4-(2t-4)=8-2t.过P作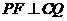，则PF=4.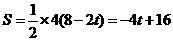

　 又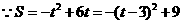开口向下对称轴为t=3,

∴0≤t≤2时，S随t增大而增大，当t=2时，S取得最大值为8.又　 ∵S=-4t+16,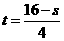

2<t≤4 ∴2<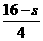≤4≥0,∴S的值不可能超过正方形面积的一半8.

本资料由《七彩教育网》 提供！

24. 解:(1)如图, ,;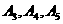

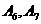(2)特殊四边形有菱形(四边形);

　 特殊三角形:直角三角形,等腰三角形,等腰直角三角形;

　(3)求证:四边形是菱形.

　证明:∵,,⊥,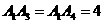

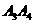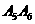　 ∴四边形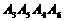是菱形