
题目列表(包括答案和解析)
2.计算: 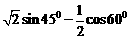 =____________.
=____________.
1.在Rt△ABC中,∠C=90°,∠A=30°,则sinB=______,tanA=_______.
24]正方形提供剪切可以拼成三角形。方法如下:

仿上面图示的方法,及韦达下列问题:
操作设计:
(1)如图(2),对直角三角形,设计一种方案,将它分成若干块,再拼成一个与原三角形等面积的矩形。
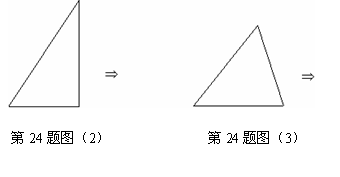
(2)如图(3)对于任意三角形,设计一种方案,将它分成若干块,再拼成一个原三角形等面积的矩形。
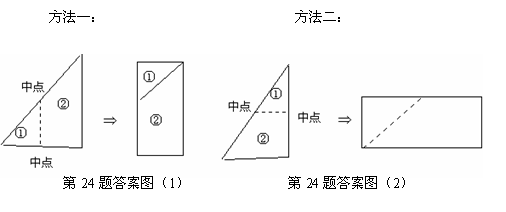 答案:(1)
答案:(1)
(2)略。
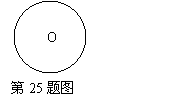 [25]如图,⊙O表示一圆形纸板,根据要求,需通过多次剪裁,把它剪成若干个扇形面,操作过程如下:第1次剪裁,将圆形纸板等分为4个扇形;第2次剪裁,将上次得到的扇形面中的一个再等分成4个扇形;以后按第2次剪裁的作法进行下去.
[25]如图,⊙O表示一圆形纸板,根据要求,需通过多次剪裁,把它剪成若干个扇形面,操作过程如下:第1次剪裁,将圆形纸板等分为4个扇形;第2次剪裁,将上次得到的扇形面中的一个再等分成4个扇形;以后按第2次剪裁的作法进行下去.
(1)请你在⊙O中,用尺规作出第2次剪裁后得到的7个扇形(保留痕迹,不写作法).
(2)请你通过操作和猜想,将第3、第4和第n次裁剪后所得扇形的总个数(S)填入下表.
|
等分圆及扇形面的次数(n) |
1 |
2 |
3 |
4 |
… |
n |
|
所得扇形的总个数(S) |
4 |
7 |
|
|
… |
|
(3)请你推断,能不能按上述操作过程,将原来的圆形纸板剪成33个扇形?为什么?
答案:(1)由图知六边形各内角相等.
(2) 七边形是正七边形.
(3)猜想:当边数是奇数时(或当边数是3,5,7,9,…时),各内角相等的圆内接多边形是正多边形.
 [26]如图,若把边长为1的正方形ABCD的四个角(阴影部分)剪掉,得一四边形A1B1C1D1.试问怎样剪,才能使剩下的图形仍为正方形,且剩下图形的面积为原正方形面积的
[26]如图,若把边长为1的正方形ABCD的四个角(阴影部分)剪掉,得一四边形A1B1C1D1.试问怎样剪,才能使剩下的图形仍为正方形,且剩下图形的面积为原正方形面积的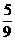 ,请说明理由(写出证明及计算过程).
,请说明理由(写出证明及计算过程).
答案:剪法是:当AA1=BB1=CC1=DD1=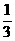 或
或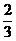 时,
时,
四边形A1B1C1D1为正方形,且S=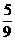 .
.
在正方形ABCD中,
AB=BC=CD=DA=1,
∠A=∠B=∠C=∠D=90°.
∵AA1=BB1=CC1=DD1,
∴A1B=B1C=C1D=D1A.
∴△D1AA1≌△A1BB1≌△B1CC1≌△C1DD1.
∴D1A1=A1B1=B1C1=C1D1,
∴∠AD1A1=∠BA1B1=∠CB1C1=∠DC1D1.
∴∠AA1D+∠BA1B1=90°,即∠D1A1B1=90°.
∴四边形A1B1C1D1为正方形.设AA1=x,
则AD1=1-x.
∵正方形A1B1C1D1的面积=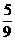 ,
,
∴S△AA1D1=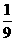
即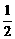 x(1-x)=
x(1-x)=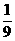 ,
,
整理得9x2-9x+2=0.
解得x1=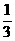 ,x2=
,x2=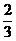 .
.
当AA1=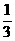 时,AD1=
时,AD1=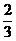 ,
,
当AA1=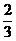 时,AD1=
时,AD1=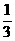 .
.
∴当AA1=BB1=CC1=DD1=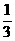 或
或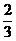 时,
时,
四边形A1B1C1D1仍为正方形且面积是原面积的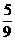 .
.
本资料由《七彩教育网》 提供!
22]电脑CPU蕊片由一种叫“单晶硅”的材料制成,未切割前的单晶硅材料是一种薄型圆片,叫“晶圆片”。现为了生产某种CPU蕊片,需要长、宽都是1cm 的正方形小硅片若干。如果晶圆片的直径为10.05cm。问一张这种晶圆片能否切割出所需尺寸的小硅片66张?请说明你的方法和理由。(不计切割损耗)
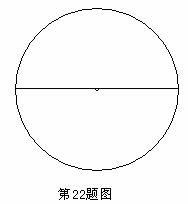
答案:可以切割出66个小正方形。
方法一:
(1)我们把10个小正方形排成一排,看成一个长条形的矩形,这个矩形刚好能放入直径为10.05cm 的圆内,如图中矩形ABCD。
∵AB=1 BC=10
∴对角线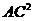 =100+1=101<
=100+1=101<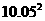
(2)我们在矩形ABCD的上方和下方可以分别放入9个小正方形。

∵新加入的两排小正方形连同ABCD的一部分可看成矩形EFGH,矩形EFGH的长为9,高为3,对角线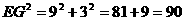 <
<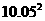 。但是新加入的这两排小正方形不能是每排10个,因为:
。但是新加入的这两排小正方形不能是每排10个,因为:
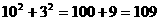 >
>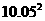
(3)同理: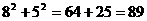 <
<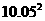
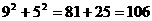 >
>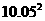
∴可以在矩形EFGH的上面和下面分别再排下8个小正方形,那么现在小正方形已有了5层。
(4)再在原来的基础上,上下再加一层,共7层,新矩形的高可以看成是7,那么新加入的这两排,每排都可以是7个但不能是8个。
∵ <
<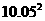
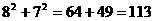 >
>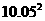
(5)在7层的基础上,上下再加入一层,新矩形的高可以看成是9,这两层,每排可以是4个但不能是5个。
∵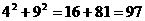 <
<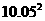
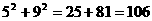 >
>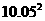
现在总共排了9层,高度达到了9,上下各剩下约0.5cm 的空间,因为矩形ABCD的位置不能调整,故再也放不下一个小正方形了。
∴10+2×9+2×8+2×7+2×4=66(个)
方法二:
学生也可能按下面的方法排列,只要说理清楚,评分标准参考方法一。
可以按9个正方形排成一排,叠4层,先放入圆内,然后:
(1)上下再加一层,每层8个,现在共有6层。
(2)在前面的基础上,上下各加6个,现在共有8层。
(3)最后上下还可加一层,但每层只能是一个,共10层。
这样共有:4×9+2×8+2×6+2×1=66(个)
 [23]在一张长12cm、宽5cm的矩形纸片内,要折出一个菱形.李颖同学按照取两组对边中点的方法折出菱形EFGH(见方案一),张丰同学沿矩形的对角线AC折出∠CAE=∠DAC,∠ACF=∠ACB的方法得到菱形AECF(见方案二),请你通过计算,比较李颖同学和张丰同学的折法中,哪种菱形面积较大?
[23]在一张长12cm、宽5cm的矩形纸片内,要折出一个菱形.李颖同学按照取两组对边中点的方法折出菱形EFGH(见方案一),张丰同学沿矩形的对角线AC折出∠CAE=∠DAC,∠ACF=∠ACB的方法得到菱形AECF(见方案二),请你通过计算,比较李颖同学和张丰同学的折法中,哪种菱形面积较大?
答案:(方案一)
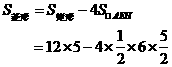
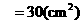
(方案二)
设BE=x,则CE=12-x
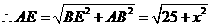
由AECF是菱形,则AE2=CE2
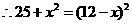
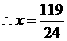
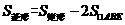
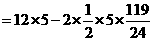
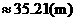
比较可知,方案二张丰同学所折的菱形面积较大.
21]用剪刀将形状如图1所示的矩形纸片ABCD沿着直线CM剪成两部分,其中M为AD的中点.用这两部分纸片可以拼成一些新图形,例如图2中的Rt△BCE就是拼成的一个图形.

(1)用这两部分纸片除了可以拼成图2中的Rt△BCE外,还可以拼成一些四边形.请你试一试,把拼好的四边形分别画在图3、图4的虚框内.
(2)若利用这两部分纸片拼成的Rt△BCE是等腰直角三角形,设原矩形纸片中的边AB和BC的长分别为a厘米、b厘米,且a、b恰好是关于x的方程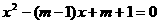 的两个实数根,试求出原矩形纸片的面积.
的两个实数根,试求出原矩形纸片的面积.
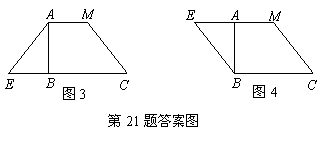
答案:(1)如图
(2)由题可知AB=CD=AE,又BC=BE=AB+AE
∴BC=2AB, 即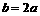
由题意知 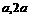 是方程
是方程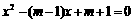 的两根
的两根
∴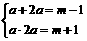
消去a,得 
解得 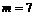 或
或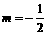
经检验:由于当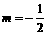 ,
,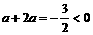 ,知
,知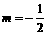 不符合题意,舍去.
不符合题意,舍去.
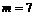 符合题意.
符合题意.
∴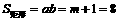
答:原矩形纸片的面积为8cm2.
19]将正方形ABCD折叠,使顶点A与CD边上的点M重合,折痕交AD于E,交BC于F,边AB折叠后与BC边交于点G(如图).
(1)如果M为CD边的中点,求证:DE∶DM∶EM=3∶4∶5;
(2)如果M为CD边上的任意一点,设AB=2a,问△CMG的周长是否与点M的位置有关?若有关,请把△CMG的周长用含DM的长x的代数式表示;若无关,请说明理由.
答案:(1)先求出DE=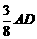 ,
,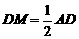 ,
,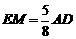 后证之.
后证之.
(2)注意到△DEM∽△CMG,求出△CMG的周长等于4a,从而它与点M在CD边上的位置无关.
18]如图,一张矩形报纸ABCD的长AB=a cm,宽BC=b cm,E、F分别是AB、CD的中点,将这张报纸沿着直线EF对折后,矩形AEFD的长与宽之比等于矩形ABCD的长与宽之比,则a∶b等于( ).
 A.
A.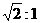 B.
B.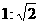 C.
C.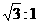 D.
D.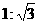

答案:A
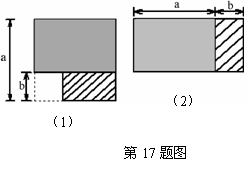
17]从边长为a的正方形内去掉一个边长为b的小正方形(如图1),然后将剩余部分剪拼成一个矩形(如图2),上述操作所能验证的等式是( )
A.a2 – b2 =(a +b)(a -b) B.(a – b)2 = a2 –2ab+ b2
C.(a + b)2 = a2 +2ab+ b2 D.a2 + ab = a (a +b)
答案:A
 [15]亲爱的同学们,在我们的生活中处处有数学的身影.请看图,折叠一张三角形纸片,把三角形的三个角拼在一起,就得到一个著名的几何定理,请你写出这一定理的结论:“三角形的三个内角和等于_______°.”
[15]亲爱的同学们,在我们的生活中处处有数学的身影.请看图,折叠一张三角形纸片,把三角形的三个角拼在一起,就得到一个著名的几何定理,请你写出这一定理的结论:“三角形的三个内角和等于_______°.”
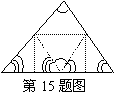

答案:180
16]如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则与 之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是( )
A. B.
C. D. 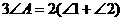
答案:B
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com