
题目列表(包括答案和解析)
6、池塘中放养了鲤鱼8000条,鲢鱼若干。在几次随机捕捞中,共抓到鲤鱼320条,鲢鱼400条。估计池塘中原来放养了鲢鱼__________条。
5.如图5,用一条宽相等的足够长的纸条,打一个结,如图(1)所示,然后轻轻拉紧、压平就可以得到如图(2)所示的正五边形ABCDE,其中∠BAC= ( )度。
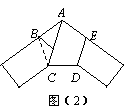 A 30 B 36 C 40 D 72
A 30 B 36 C 40 D 72


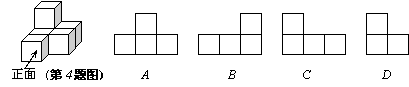
4.如图所示是由几个小正方体组成的一个几何体,这个几何体的左视图是( ).
3、四个小朋友玩跷跷板,他们的体重分别为P、Q、R、S,
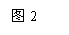 如图3所示,则他们的体重大小关系是( )
如图3所示,则他们的体重大小关系是( )


A  B
B 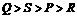 C
C 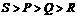 D
D 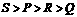
1将图1按顺时针方向旋转90°后得到的是( )

2、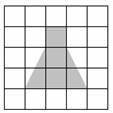 如图2,每个小正方形的边长为1,把阴影部分剪下来,用
如图2,每个小正方形的边长为1,把阴影部分剪下来,用
剪下来的阴影部分拼成一个正方形,那么新正方形的边长是( )
A 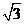 B 2 C
B 2 C
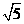 D
D 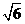
25.(本题满分12分)已知:在Rt△ABO中,∠OAB=90°,∠BOA=30°,AB=2,若以O为坐标原点,OA所在直线为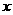 轴,建立如图所示平面直角坐标系,点B在第一象限内,将Rt△ABO沿OB折叠后,点A落在第一象限内的点C处.
轴,建立如图所示平面直角坐标系,点B在第一象限内,将Rt△ABO沿OB折叠后,点A落在第一象限内的点C处.
(1)求点C的坐标;(3分)
(2)若抛物线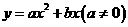 经过C、A两点,求此抛物线的解析式;(4分)
经过C、A两点,求此抛物线的解析式;(4分)
(3)若上述抛物线的对称轴与OB交于点D,点P为线段DB上一动点,过P作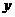 轴的平行线,交抛物线于点M,问:是否存在这样的点P,使得四边形CDPM为很等腰梯形?若存在,请求出此时点P的坐标;若不存在,请说明理由. (5分)
轴的平行线,交抛物线于点M,问:是否存在这样的点P,使得四边形CDPM为很等腰梯形?若存在,请求出此时点P的坐标;若不存在,请说明理由. (5分)

24. (本题满分10分)宏达纺织品有限公司准备投资开发A、B两种新产品,通过市场调研发现:如果单独投资A种产品,则所获利润(万元)与投资金额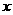 (万元)之间满足正比例函数关系:
(万元)之间满足正比例函数关系: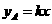 ;如果单独投资B种产品,则所获利润(万元)与投资金额
;如果单独投资B种产品,则所获利润(万元)与投资金额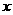 (万元)之间满足二次函数关系:
(万元)之间满足二次函数关系: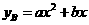 .根据公司信息部的报告,
.根据公司信息部的报告,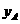 ,
,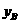 (万元)与投资金额
(万元)与投资金额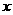 (万元)的部分对应值(如下表)
(万元)的部分对应值(如下表)
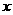 |
1 |
5 |
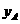 |
0.6 |
3 |
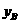 |
2.8 |
10 |
(1)填空:(4分)
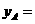 _______________________;
_______________________;
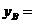 _______________________;
_______________________;
(2)如果公司准备投资20万元同时开发A、B两种新产品,设公司所获得的总利润为 (万元),试写出
(万元),试写出 与某种产品的投资金额x之间的函数关系式.(3分)
与某种产品的投资金额x之间的函数关系式.(3分)
(3)请你设计一个在(2)中能获得最大利润的投资方案,并求出按此方案能获得的最大利润是多少万元?(3分)
23. (本题满分12分)如图,在Rt△ABC中,∠ACB=90°,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于点E.
(1)求证:点E是边BC的中点;(4分)
(2)若EC=3,BD=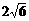 ,求⊙O的直径AC的长度;(4分)
,求⊙O的直径AC的长度;(4分)
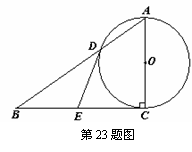 (3)若以点O,D,E,C为顶点的四边形是正方形,试判断△ABC的形状,并说明理由. (4分)
(3)若以点O,D,E,C为顶点的四边形是正方形,试判断△ABC的形状,并说明理由. (4分)
22.(本题满分9分)定理:若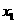 、
、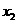 是关于
是关于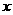 的一元二次方程
的一元二次方程 的两实根,则有
的两实根,则有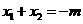 ,
,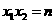 .请用这一定理解决问题:已知
.请用这一定理解决问题:已知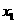 、
、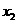 是关于
是关于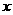 的一元二次方程
的一元二次方程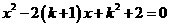 的两实根,且
的两实根,且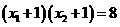 ,求
,求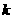 的值.
的值.
21.(本题满分9分)一个不透明的口袋里装着红、黄、绿三种只有颜色不同的球,其中红球有2个,黄球有1个,从中任意摸出1球是红球的概率为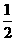 .
.
(1)试求袋中绿球的个数;(4分)
(2)第1次从袋中任意摸出l球(不放回),第2次再任意摸出1球,请你用画树状图或列表格的方法,求两次都摸到红球的概率. (5分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com