
题目列表(包括答案和解析)
1.下列判定四边形是平行四边形的方法中,错误的是( )
A.一组对边平行,一组对角相等 B.一组对边平行,另一组对边相等
C.两组对边分别相等 D.两组对角分别相等
|
内容 |
质 量 |
广 告 |
价 格 |
||||||
|
品牌 |
A |
B |
C |
A |
B |
C |
A |
B |
C |
|
满意户数 |
194 |
121 |
117 |
163 |
172 |
107 |
98 |
96 |
100 |
根据上述信息回答下列问题:
(1)A品牌洗衣粉的主要竞争优势是什么?你是怎样看出来的?
(2)广告对用户选择品牌有影响吗?请简要说明理由。
(3)你对厂家和何建议?
本资料由《七彩教育网》 提供!
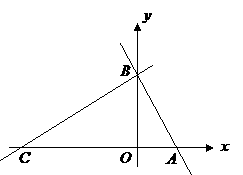
27.(本题满分12分)如图,在平面直角坐标系中,点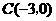 ,点
,点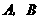 分别在
分别在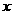 轴,
轴,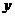 轴的正半轴上,且满足
轴的正半轴上,且满足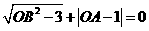 .
.
(1)求点 ,点
,点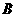 的坐标.
的坐标.
(2)若点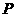 从
从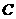 点出发,以每秒1个单位的速度沿射线
点出发,以每秒1个单位的速度沿射线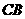 运动,连结
运动,连结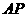 .设
.设 的面积为
的面积为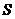 ,点
,点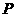 的运动时间为
的运动时间为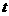 秒,求
秒,求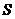 与
与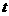 的函数关系式,并写出自变量的取值范围.
的函数关系式,并写出自变量的取值范围.
 (3)在(2)的条件下,是否存在点
(3)在(2)的条件下,是否存在点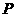 ,使以点
,使以点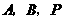 为顶点的三角形与
为顶点的三角形与 相似?若存在,请直接写出点
相似?若存在,请直接写出点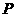 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
命题人:张鹏飞 学校:沭阳县修远中学 校对:姜进
宿迁市2008-2009学年度下学期普通中学第一次四校联考
26.(本题满分12分)宏达纺织品有限公司准备投资开发A、B两种新产品,通过市场调研发现:如果单独投资A种产品,则所获利润(万元)与投资金额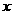 (万元)之间满足正比例函数关系:
(万元)之间满足正比例函数关系: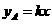 ;如果单独投资B种产品,则所获利润(万元)与投资金额
;如果单独投资B种产品,则所获利润(万元)与投资金额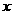 (万元)之间满足二次函数关系:
(万元)之间满足二次函数关系: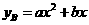 .根据公司信息部的报告,
.根据公司信息部的报告,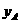 ,
,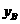 (万元)与投资金额
(万元)与投资金额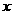 (万元)的部分对应值(如下表)
(万元)的部分对应值(如下表)
(1)填空:
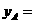 _______________________;
_______________________;
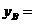 _______________________;
_______________________;
(2)如果公司准备投资20万元同时开发A、B两种新产品,设公司所获得的总利润为 (万元),试写出
(万元),试写出 与某种产品的投资金额x之间的函数关系式.
与某种产品的投资金额x之间的函数关系式.
(3)请你设计一个在(2)中能获得最大利润的投资方案,并求出按此方案能获得的最大利润是多少万元?
25.(本题满分12分)在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20只,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,再把它放回袋中,不断重复.下表是活动进行中的一组统计数据:
摸球的次数 |
100 |
150 |
200 |
500 |
800 |
1000 |
摸到白球的次数 |
58 |
96 |
116 |
295 |
484 |
601 |
摸到白球的频率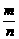 |
0.58 |
0.64 |
0.58 |
0.59 |
0.605 |
0.601 |
⑴请估计:当n很大时,摸到白球的频率将会接近 ;
⑵试估算口袋中黑、白两种颜色的球各有多少只?
⑶请画树状图或列表计算:从中一次摸两只球,这两只球颜色不同的概率是多少?
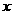 |
1 |
5 |
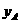 |
0.6 |
3 |
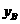 |
2.8 |
10 |
24.(本题满分12分) 如图,一次函数
如图,一次函数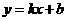 的图象与反比例函数
的图象与反比例函数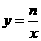 的图象相交于A、B两点.
的图象相交于A、B两点.
⑴利用图中的条件,求反比例函数和一次函数的关系式;
⑵若经过点A、B的抛物线与y轴相交于点C,且△ABC
的面积为12,求点C的坐标.
23.(本题满分12分)已知:如图,在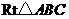 中,
中,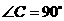 ,点
,点 在
在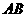 上,以
上,以 为圆心,
为圆心, 长为半径的圆与
长为半径的圆与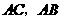 分别交于点
分别交于点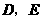 ,且
,且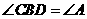 .
.
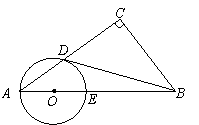 (1)判断直线
(1)判断直线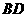 与
与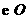 的位置关系,并证明你的结论;
的位置关系,并证明你的结论;
(2)若 ,
,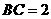 ,求
,求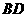 的长.
的长.
.
22.(本题满分12分)已知一元二次方程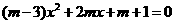 有两个不相等的实数根,并且这两个根又不互为相反数.
有两个不相等的实数根,并且这两个根又不互为相反数.
(1)求 的取值范围;
的取值范围;
(2)当 在取值范围内取最小偶数时,求方程的根.
在取值范围内取最小偶数时,求方程的根.
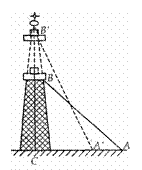
21.(本题满分8分)已知电视发射塔BC,为稳固塔身,周围拉有钢丝地锚线(如图线段AB),若AB=60m,并且AB与地面成45°角,欲升高发射塔的高度到CB′,同时原地锚线仍使用,若塔升高后使地锚线与地面成60°角,求电视发射塔升高了多少米?(即BB′的高度)
20.(本题满分8分)化简代数式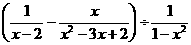 ,然后请你取一个你喜欢的x的值代入求值。
,然后请你取一个你喜欢的x的值代入求值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com