
题目列表(包括答案和解析)
5、为了估计池塘里有多少条鱼,从池塘里捕捞了1000条鱼做上标记,然后放回池塘里,经过一段时间,等有标记的鱼完全混合于鱼群中以后,再捕捞200条,若其中有标记的鱼有5条,则估计池塘里有鱼( ).
(A)5000条 (B)10000条 (C)20000条 (D)40000条
4、同时抛掷两枚1元的硬币,菊花图案都朝上的概率是( ).
(A)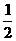 (B)
(B)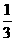 (C)
(C)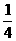 (D)
(D)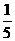
3、在△ABC中,若∠C= 90°,AC=1,BC=2,则下列结论中正确的是( ).
(A)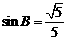 (B)
(B)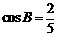 (C)
(C)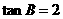 (D)tanA=
(D)tanA=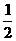
2、对于反比例函数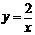 ,下列说法中不正确的是( ).
,下列说法中不正确的是( ).
(A)点(-2,-1)在它的图象上 (B)它的图象在第一、三象限
(C)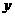 随
随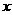 的增大而减小 (D)当x<0时,
的增大而减小 (D)当x<0时,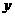 随
随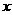 的增大而减小
的增大而减小
1、将方程x2+4x+2=0配方后,原方程变形为( ).
(A)(x+2)2 =2 (B)(x+4)2 =3
(C)(x+2)2 =-3 (D)(x+2)2=-5
25、(本小题满分8分)
如图,抛物线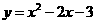 与
与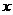 轴交A、B两点(A点在B点左侧),直线
轴交A、B两点(A点在B点左侧),直线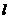 与抛物线交于A、C两点,其中C点的横坐标为2。
与抛物线交于A、C两点,其中C点的横坐标为2。
(1)求A、B 两点的坐标及直线AC的函数表达式;
(2)P是线段AC上的一个动点,过P点作y轴的平行线交抛物线于E点,求线段PE长度的最大值;
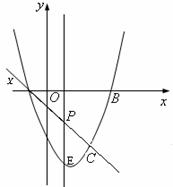 (3)点G抛物线上的动点,在x轴上是否存在点F,使A、C、F、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由(请直接写出点的坐标,不要求写过程)。
(3)点G抛物线上的动点,在x轴上是否存在点F,使A、C、F、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由(请直接写出点的坐标,不要求写过程)。
(第25题图)
北京市宣武区2008-2009学年度第一学期期末质量检测
24.(本小题满分7分)
已知⊙O过点D(4,3),点H与点D关于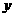 轴对称,过H作⊙O的切线交
轴对称,过H作⊙O的切线交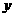 轴于点A(如图1)。
轴于点A(如图1)。
⑴求⊙O半径;
⑵求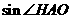 的值;
的值;
⑶如图2,设⊙O与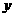 轴正半轴交点P,点E、F是线段OP上的动点(与P点不重合),联结并延长DE、DF交⊙O于点B、C,直线BC交
轴正半轴交点P,点E、F是线段OP上的动点(与P点不重合),联结并延长DE、DF交⊙O于点B、C,直线BC交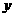 轴于点G,若
轴于点G,若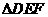 是以EF为底的等腰三角形,试探索
是以EF为底的等腰三角形,试探索 的大小怎样变化?请说明理由。
的大小怎样变化?请说明理由。
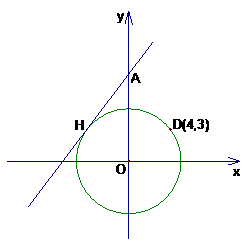
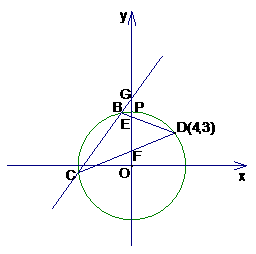
图1 图2
(第24题图)
23.(本小题满分6分)
如图,在平面直角坐标系中,直线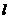 是第一、三象限的角平分线.
是第一、三象限的角平分线.
实验与探究:
(1)
由图观察易知A(0,2)关于直线l的对称点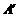 的坐标为(2,0),请在图中分别标明
的坐标为(2,0),请在图中分别标明
B(5,3) 、C(-2,5) 关于直线l的对称点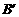 、
、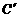 的位置,并写出他们的坐标:
的位置,并写出他们的坐标: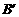 、
、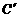 ;
;
归纳与发现:
(2)
结合图形观察以上三组点的坐标,你会发现:坐标平面内任一点P(a,b)关于第一、三象限的角平分线l的对称点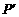 的坐标为
(不必证明);
的坐标为
(不必证明);
运用与拓广:
(3)
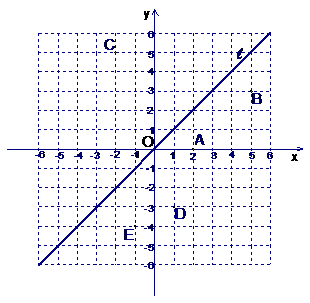 已知两点D(1,-3)、E(-1,-4),试在直线l上确定一点Q,使点Q到D、E两点的距离之和最小,并求出Q点坐标.
已知两点D(1,-3)、E(-1,-4),试在直线l上确定一点Q,使点Q到D、E两点的距离之和最小,并求出Q点坐标.
(第23题图)
22.(本小题满分6分)
我市某工艺厂为配合北京奥运,设计了一款成本为20元∕件的工艺品投放市场进行试销.
经过调查,得到如下数据:
销售单价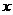 (元∕件) (元∕件) |
…… |
30 |
40 |
50 |
60 |
…… |
每天销售量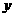 (件) (件) |
…… |
500 |
400 |
300 |
200 |
…… |
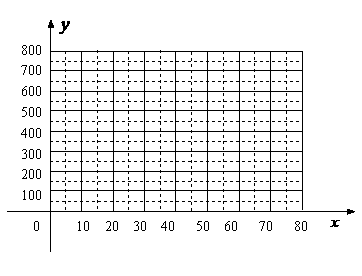
(1)把上表中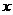 、
、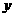 的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想
的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想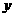 与
与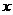 的函数关系,并求出函数关系式;
的函数关系,并求出函数关系式;
(2)当销售单价定为多少时,工艺厂试销该工艺品每天获得的利润最大?最大利润是多少?
 (利润=销售总价-成本总价);
(利润=销售总价-成本总价);
21.(本小题满分6分)
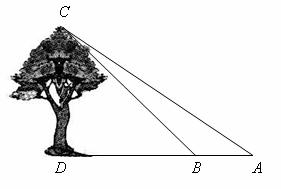
在数学活动课上,九年级(1)班数学兴趣小组的同学们测量校园内一棵大树的高度,设计的方案及测量数据如下:
(1)在大树前的平地上选择一点 ,测得由点A看大树顶端
,测得由点A看大树顶端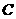 的仰角为35°;
的仰角为35°;
(2)在点 和大树之间选择一点
和大树之间选择一点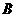 (
( 、
、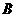 、
、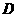 在同一直线上),测得由点
在同一直线上),测得由点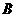 看大树顶端
看大树顶端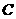 的仰角恰好为45°;
的仰角恰好为45°;
(3)量出 、
、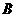 两点间的距离为4.5米.请你根据以上数据求出大树
两点间的距离为4.5米.请你根据以上数据求出大树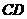 的高度.
的高度.
 (可能用到的参考数据:sin35°≈0.57
cos35°≈0.82 tan35°≈0.70)
(可能用到的参考数据:sin35°≈0.57
cos35°≈0.82 tan35°≈0.70)
(第21题图)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com