1．求满足下列等式的x的值．

　①5x²-15x＝0

　②5x(x-2)-4(2-x)＝0

　(1)x(x-y)-y(y-x)

　(2)-12x³+12x²y-3xy²

　(3)(x+y)²+mx+my

　(4)a(x-a)(x+y)²-b(x-a)²(x+y)

　(1)多项式8x^my^n-1-12x^3myⁿ的公因式是(　)

　A．x^myⁿ B．x^my^n-1 　C．4x^myⁿ D．4x^my^n-1

　(2)把多项式-4a³+4a²-16a分解因式(　)

　A．-a(4a²-4a+16)　　　　　　　　　　　　　　　　　　　　　　　　 B．a(-4a²+4a-16)

　C．-4(a³-a²+4a)　　　　　　　　　　　　　　　　　　　　　　　　　 D．-4a(a²-a+4)

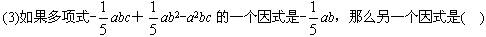
　A．c-b+5ac　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B．c+b-5ac

　C．c-b+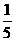ac　　　　　　　　　　　　　　　　　　　　　　　　　　　　 D．c+b-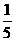ac

　(4)用提取公因式法分解因式正确的是(　)

　A．12abc-9a²b²＝3abc(4-3ab)

　B．3x²y-3xy+6y＝3y(x²-x+2y)

　C．-a²+ab-ac＝-a(a-b+c)

　D．x²y+5xy-y＝y(x²+5x)

　(1)单项式-12x¹²y³与8x¹⁰y⁶的公因式是________．

　(2)-xy²(x+y)³+x(x+y)²的公因式是________．

　(3)把4ab²-2ab+8a分解因式得________．

　(4)5(m-n)⁴-(n-m)⁵可以写成________与________的乘积．

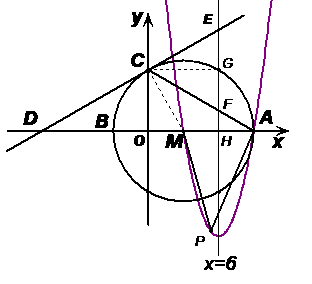
25．(12分)解：(1)连接CM，由题意得：OM=3，OB=3，OE=9，MC=6

OA=OM+MA=3+6=9

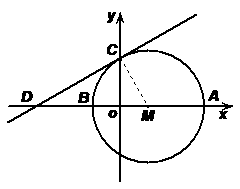A(9，0)……………………………………1分

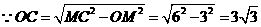
∴C(0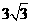，)……………………………………2分

(2)证法一：

在Rt△DCO中，

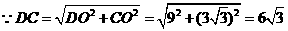
在△DCM中，

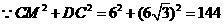
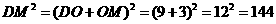
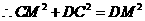……………………………………3分

∴△DCM直角三角形。……………………………………4分

∴MC⊥DC，而MC是⊙M的半径

∴CD是⊙M的切线。……………………………………5分

证法二：

在Rt△COM中，

……………………………………3分

在Rt△DOC中，

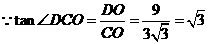
……………………………………4分

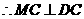，而MC中的⊙M半径。……………………………………5分

证法三：

在△CMO和△DMC中

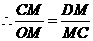……………………………………3分

又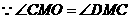

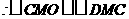……………………………………4分

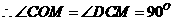
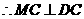，而MC中的⊙M半径。

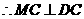，而MC中的⊙M半径。……………………………………5分

(3)由抛物线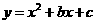经过点M(3，0)和点A(9，0)，可得：

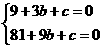　　 解得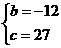：……………………………………6分

∴抛物线的解析式为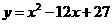： ……………………………………7分

(4)存在。……………………………………8分

方法一：

设直线CD的解析式为，点C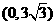和点D(-9，0)在此直线上，可得：

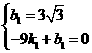　　　　 解得：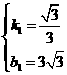

∴直线CD的解析式为：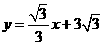

设直线AC的解析式为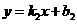，点A(9，0)和点C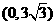在此直线上，可得：

解得：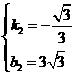

∴直线AC的解析式为：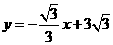

∵抛物线的对称轴为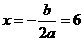

又∵点E是对称轴和直线CD的交点

当x=6时，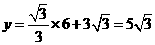

点E的坐标为(6，)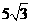

双点F是对称轴和直线AC交点

∴当x=6时，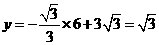

∴点F的坐标为(6，)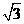

∴

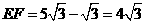
过点C作CG⊥EF于点G，则CG=6

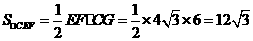
①　　 若点P在轴的上方，设点P坐标为(x，y)

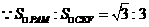
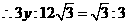
解得：y=4

当y=4时，即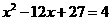，解得

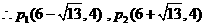……………………………………10分

②若点P在x轴上，则点P与点M或与点A重合，此时构不成三角形。

③若点P在x轴下方，设点P的坐标为(x，y)

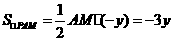
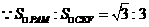
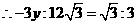
解得：y=－4

当y=－4时，即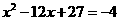，解得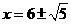

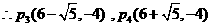……………………………………12分

∴这样的点共有4个，，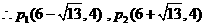

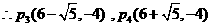
方法二：存在……………………………………8分

设抛物线的对称轴交x轴于点H

在(2)中已证：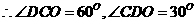

∵抛物线的对称轴平行于y轴

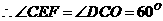
∵OD=OA=9

∴CO垂直平分AD

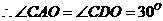
在Rt△AFH中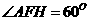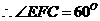，　　 　　∴△CEF是等边三角形

过点C作CG⊥EF于点G，则CG=6

可得：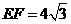

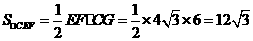
以下解答与方法一相同。　　 (本题其它解法参照此标准给分)

本资料由《七彩教育网》 提供！

24、解：(1)根据题意得：

解得：

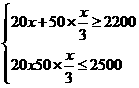……………………………………2分

解得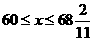：……………………………………3分

∵x为正整数∴x可取60，61，62，63，64，65，66，67，68

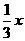∵也必需是整数∴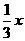可取20，21，22……………………………………4分

∴有三种购买方案：

方案一：跳绳60根，排球20个：

方案二：跳绳63根，排球21个：

方案一：跳绳66根，排球22个：……………………………………5分

(2)在(1)中，方案一购买的总数量最少，所以总费用最少

最少费用为：60×20+20×50=220……………………………………6分

(3)设用(2)中的最少费用最多还可以多买的排球数量为y，

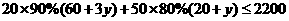……………………………………7分

解得：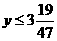

∵y为正整数∴满足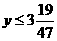的最大正整数为3

∴多买的跳绳为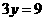：(根)……………………………………8分

答：用(2)中的最少费用最多还可以多买9根跳绳和3个排球。………………………9分

23、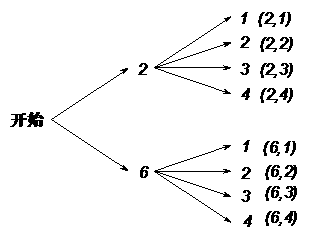解：(1)树状图如下：

列表如下：

列表如下：

备注：此小题4分，画对图1(表2)得2分，结果写对得2分。

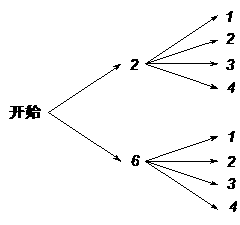图1

表1

(2)所有的总分为：3，4，5，6，7，8，9，10。

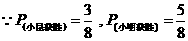
∴ 游戏不公平

22、解：(1)由图象可知，y是x的一次函数，

设此一次函数的解析式为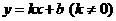：………………1分

点和点是一次函数图象上

∵点(0，2000)和点(20，0)在一次函数上。

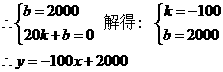………………3分

自变量的取值范围是：0≤x≤20 ………………4分

(2)当x=15时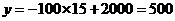，………………5分

∵ 500＜3×180………………6分

∴剩余的果汁不够倒满每个容积为180毫升的3个纸杯。………………7分

21、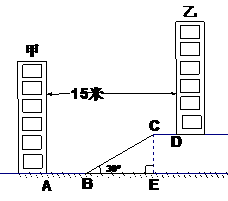解：过点C作CE⊥地面于点E ………………1分

∵两楼水平距离为15米，

且AB=2米，CD=4米

∴BE=15－2－4=9米………………2分

在Rt△ABC中，

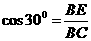………………3分

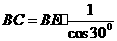………………4分

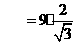………………5分

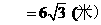………………6分

答：斜坡BC的长度为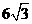米………………7分

20、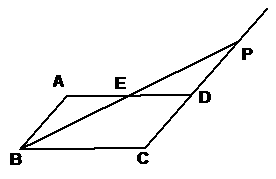解：当PD=CD时，△ABE≌△DPE……1分

画出图形如下：…………………………2分

证明：∵四边形ABCD是平行四边形

∴AB=CD。AB∥CD………………………3分

∴∠BAE=∠PDE…………………………4分

又∵PD=CD

∴AB=DP……………………………………5分

在△ABE和△DPE中

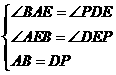…………………………6分

∴△ABE≌△DPE中(AAS)……………………………………7分

(本题其它证明方法参照此标准给分)