
题目列表(包括答案和解析)
6.一次函数y=mx+n的图象如图所示,那么二次函数y=nx2+mx的图象大致为 ( )

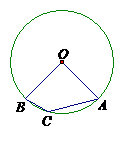
5. 已知二次函数
已知二次函数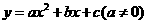 的图象如图所示,当
的图象如图所示,当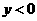
时, 的取值范围是( )
的取值范围是( )
A.
B.
C.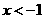
D. 或
或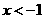
4.关于二次函数y=x2+4x-7的最大(小)值,叙述正确的是 ( )
A.当x=2时,函数有最大值 B.x=2时,函数有最小值
C.当x=-1时,函数有最大值 D.当x=-2时,函数有最小值
3.函数y=x2-2x+3的图象的顶点坐标是 ( )
A.(1,-4) B.(-1,2) C.(1,2) D.(0,3)
2.下列图形中既是中心对称图形又是轴对称图形的是 ( )

A B C D
1.抛物线y=(x-2)2+3的对称轴是 ( )
A.直线x=-3 B.直线x=3 C.直线x=-2 D.直线x=2
28.如图1,三角形纸片 ,
, .沿
.沿 边上的高
边上的高 把这张纸片剪成
把这张纸片剪成 和
和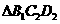 (图2).将
(图2).将 沿直线
沿直线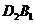 方向向右平移(点
方向向右平移(点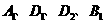 始终共线),在平移过程中,
始终共线),在平移过程中, 交
交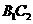 于
于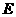 ,
,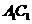 分别交
分别交 、
、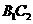 于
于 ,设平移距离
,设平移距离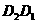 为
为 ,
, 与
与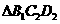 重叠部分的面积为
重叠部分的面积为 .
.
(1)当点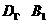 重合时,停止平移(如图3).请用
重合时,停止平移(如图3).请用 表示出
表示出 的面积,并求出
的面积,并求出 与
与 的函数关系式(写出自变量
的函数关系式(写出自变量 的取值范围).
的取值范围).
(2)当点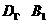 重合后,将纸片
重合后,将纸片 沿直线
沿直线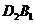 方向继续向右平移,一直到点
方向继续向右平移,一直到点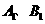 重合时停止平移(如图4和图5).其余条件不变,请求出
重合时停止平移(如图4和图5).其余条件不变,请求出 与
与 的函数关系式(写出自变量
的函数关系式(写出自变量 的取值范围).
的取值范围).
(3)利用(1)、(2)的结论,试分析:当 为何值时,面积
为何值时,面积 最大?最大面积是多少?
最大?最大面积是多少?


27.如图,抛物线 经过
经过 的三个顶点,已知
的三个顶点,已知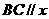 轴,点
轴,点 在
在 轴上,点
轴上,点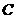 在
在 轴上,且
轴上,且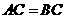 .
.
(1)求抛物线的对称轴;
(2)求出 三点的坐标,并求抛物线的解析式;
三点的坐标,并求抛物线的解析式;
(3)探究:若点 为(2)中抛物线上第一象限内一点,过点
为(2)中抛物线上第一象限内一点,过点 作
作 轴于点
轴于点 ,问是否存在这样的点
,问是否存在这样的点 ,使
,使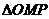 ∽
∽ (其中
(其中 )?若存在,求出所有符合条件的点
)?若存在,求出所有符合条件的点 坐标;若不存在,请说明理由.
坐标;若不存在,请说明理由.
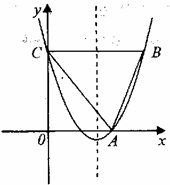
26.一座拱桥的轮廓是抛物线型(如图1),拱高6m,跨度20m,相邻两支柱间的距离均为5m,拱桥下地平面是双向行车道(正中间是一条宽2m的隔离带),将抛物线放在所给的直角坐标系中(如图2).
(1)求抛物线的解析式;
(2)求支柱 的长度;
的长度;
(3)时值梅雨季节,我校决定调运一辆宽3m、高4m的超宽、超高货运汽车运送新棉被(棉毯)及冬衣等急需物资前往汶川地震灾区,途中要经过这座拱桥,请你预测一下货运汽车能否安全通过(汽车与隔离带的间隔忽略不计)?并说明理由.

25.已知二次函数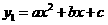 的图像经过三点
的图像经过三点 ,顶点为
,顶点为 .
.
 (1)求二次函数的解析式,并在给定的直角坐标系中作出这个函数的图像(不列表,只描出
(1)求二次函数的解析式,并在给定的直角坐标系中作出这个函数的图像(不列表,只描出 四点,再连成抛物线);
四点,再连成抛物线);
解:
(2)请你求出四边形 的面积;
的面积;
(3)若正比例函数 的图像与二次函数
的图像与二次函数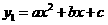 的图像在第一象限内交于点
的图像在第一象限内交于点 ,
, 落在两个相邻的正整数之间,请你观察图像,写出这两个相邻的正整数为________________;
落在两个相邻的正整数之间,请你观察图像,写出这两个相邻的正整数为________________;
(4)若正比例函数 的图像与二次函数
的图像与二次函数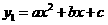 的图像在第一象限内交于点
的图像在第一象限内交于点 ,且
,且 满足
满足 ,则实数
,则实数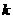 的取值范围___________________.
的取值范围___________________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com