5．如图2-4-26，在Rt△ABC中，∠ACB=90⁰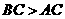，，以斜边AB所在直线为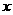轴，以斜边AB上的高所在的直线为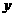轴，建立直角坐标系，若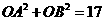，且线段OA、OB的长是关于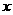的一元二次方程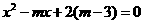的两根．(1)求点C的坐标．(2)以斜边AB为直径作圆与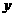轴交于另一点E，求过A、B、E三点的抛物线的解析式，并画出此抛物线的草图．(3)在抛物线的解析式上是否存在点P，使△ABP和△ABC全等？若相聚在，求出符合条件的P点的坐标；若不存在，请说明理由．

[答案]　　　　　　　　　　　　　　　　　　　　

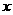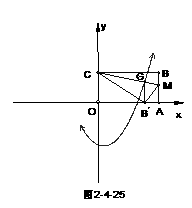
4．OABC是一张平放在直角坐标系中的矩形纸片，O为原点，点A在轴上，点C在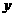轴上，OA=10，OC=6．(1)如图2-4-25，在AB上取一点M，使得△CBM沿CM翻折后，点B落在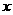轴上，记作B′点，求所B′点的坐标．(2)求折痕CM所在直线的解析式．(3)作B′G∥AB交CM于点G，若抛物线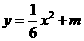过点G，求抛物线的解析式，交判断以原点O为圆心，OG为半径的圆与抛物线除交点G外，是否还有交点？若有，请直接写出交点的坐标．　　　　

3．在以O这原点的平面直角坐标系中，抛物线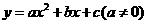与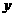轴交于点C(0，3)．与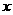轴正半轴交于A、B两点(B点在A点的右侧)，抛物线的对称轴是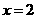，且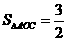．(1)求此抛物线的解析式．(2)设抛物线的顶点为D，求四边形ADBC的面积．　　　　　　　　　　　　　 　

2．如图2-4-24，已知反比例函数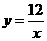的图象与一次函数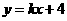的图象相交于P、Q两点，并且P点的纵坐标是6．(1)求这个一次函数的解析式．(2)求△POQ的面积．

1．已知抛物线的解析式为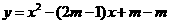，(1)求证：此抛物线与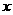轴必有两个不同的交点．(2)若此抛物线与直线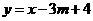的一个交点在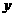轴上，求的值．

23．(本题12分)2008年北京奥运会的比赛已经圆满闭幕．当时某球迷打算用8000元预订10张下表中比赛项目的门票．(下表为当时北京奥运会官方票务网站公布的几种球类决赛的门票价格)

(1)若全部资金用来预订男篮门票和乒乓球门票，问他可以订男篮门票和乒乓球门票各多少张？

(2)若在现有资金8000元允许的范围内和总票数不变的前提下，他想预订下表中三种球类门票，其中男篮门票数与足球门票数相同，且乒乓球门票的费用不超过男篮门票的费用，求他能预订三种球类门票各多少张？

22．(本题9分)某年级组织学生参加夏令营

活动，本次夏令营分为甲、乙、丙三组进

行。

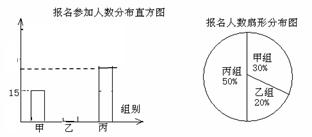
下面两幅统计图反映了学生参加夏令营的

报名情况，请你根据图中的信息回答下列

问题：

(1)该年级报名参加丙组的人数为　　　 人；

(2)该年级报名参加本次活动的总人数为　　　 人，并补全频数分布直方图；

(3)根据实际情况，需从甲组抽调部分同学到丙组，使丙组人数是甲组人数的3倍，应从甲抽调多少名学生到丙组？

21.(本题12分)

如图，在直角坐标系中，直线OA与双曲线交于点A(2,2)，求：

(1)直线OA与双曲线的函数解析式；

(2)将直线OA向上平移3个单位后，求直线与双曲线的交点C，D的坐标；

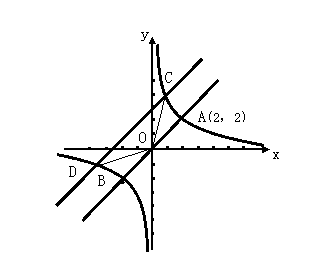(3)求△COD的面积。

20．(本题9分)在如图方格纸中，每个小方格都是边长为1个单位的正方形，△ABC的三个顶点都在格点上(每个小方格的顶点叫格点)。

(1)画出△ABC向下平移4个单位后的△A₁B₁C₁；

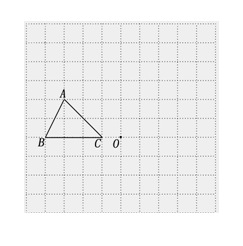(2)画出△ABC绕点O顺时针旋转90°后的△A₂B₂C₂，并求点旋转到A₂所经过的路线长。

19．(本题8分)如图，农民张大伯为了致富奔小康，大力发展家庭养殖业，他准备用40米长的木栏围一个矩形的鸡圈。为了节约材料，同时要使矩形的面积最大，他利用了自己家房屋一面，准备设计如图所示的一个矩形的养鸡圈。设养鸡圈的宽为x米，面积为y平方米。

(1)求y与x的函数关系式；

(2)怎样围，使得围成的养鸡圈面积最大，最大面积是多少？