例3(牡丹江)某工厂计划为震区生产A，B两种型号的学生桌椅500套，以解决1250名学生的学习问题，一套A型桌椅(一桌两椅)需木料0．5m3，一套B型桌椅(一桌三椅)需木料0．7m3，工厂现有库存木料302m3．

(1)有多少种生产方案？

(2)现要把生产的全部桌椅运往震区，已知每套A型桌椅的生产成本为100元，运费2元；每套B型桌椅的生产成本为120元，运费4元，求总费用y(元)与生产A型桌椅x(套)之间的关系式，并确定总费用最少的方案和最少的总费用．(总费用＝生产成本+运费)

(3)按(2)的方案计算，有没有剩余木料？如果有，请直接写出用剩余木料再生产以上两种型号的桌椅，最多还可以为多少名学生提供桌椅；如果没有，请说明理由．

分析　先利用题目中的两个不等关系，列出不等式组，确定生产方案，进而为了计算的方便，可引进一次函数，利用一次函数的性质求出最少费用，在此基础上，计算所用木料．　

解：(1)设生产A型桌椅x套，则生产B型桌椅(500－x)套，

则根据题意，得 解得240≤x≤250．

因为x是整数，所以有11种生产方案．

(2)依题意有y＝(100+2)x+(120+4)(500－x)＝－22x+62000．

由(1)可知x的值分别为240、241、…、250这11个整数，

当x＝240时，y＝－22×240+62000＝56720；当x＝241时，y＝－22×241+62000＝56698；…，当x＝250时，y＝－22×250+62000＝56500．

可知当x＝250时，y有最小值，即当生产A型桌椅250套、B型桌椅250套时，总费用最少，此时最小值为＝56500元．

(3)因为生产A型桌椅250套、B型桌椅250套共需的木料为250×0．5+250×0．7＝300(m3)，所以还剩余2m3的木料，即有剩余木料，最多还可以生产A型桌椅4套，可解决8名同学的桌椅问题．

说明　本题先是利用不等量关系，列出不等式确定生产方案，然后一环套一环地求解．

本资料由《七彩教育网》 提供！

例1(怀化市)5．12四川地震后，怀化市立即组织医护工作人员赶赴四川灾区参加伤员抢救工作．拟派30名医护人员，携带20件行李(药品、器械)，租用甲、乙两种型号的汽车共8辆，日夜兼程赶赴灾区．经了解，甲种汽车每辆最多能载4人和3件行李，乙种汽车每辆最多能载2人和8件行李．

(1)设租用甲种汽车x辆，请你设计所有可能的租车方案；

(2)如果甲、乙两种汽车的租车费用每辆分别为8000元、6000元，请你选择最省钱的租车方案．

分析　很明显，有两个不等量关系：一是甲种汽车与乙种汽车装载的人数和不少于30，二是甲种汽车与乙种汽车装载的行李和不少于20，于是，可以列出不等式组，确定租车方案，进而通过计算，并比较选择最省钱的租车方案．

解(1)因为租用甲种汽车为x辆，则租用乙种汽车(8－x)辆．

则根据题意，得 解之，得7≤x≤ ，所以x只能取整数7或8．

即共有两种租车方案：第一种是租用甲种汽车7辆，乙种汽车1辆；第二种是全部租用甲种汽车8辆．

(2)第一种租车方案的费用为7×8000+1×6000＝62000元．

第二种租车方案的费用为8×8000＝64000元．所以第一种租车方案最省钱．

说明　本题意在考查同学们对列不等式组解应用题的能力，求解时要根据条件，找出不等量关系，列出不等式组，求出满足条件的解，确定其方案，再分别求出其费用，做出决策．

例1(襄樊市)"六一"儿童节前夕，某消防队官兵了解到汶川地震灾区一帐篷小学的小朋友喜欢奥运福娃，就特意购买了一些送给这个小学的小朋友作为节日礼物．如果每班分10套，那么余5套；如果前面的班级每个班分13套，那么最后一个班级虽然分有福娃，但不足4套．问：该小学有多少个班级？奥运福娃共有多少套？

分析　抓住"如果前面的班级每个班分13套，那么最后一个班级虽然分有福娃，但不足4套"建立不等式组求解．

解　设该小学有x个班，则奥运福娃共有(10x+5)套．

则根据题意，得 解得 ＜x＜6．

因为x只能取整数，所以x＝5，此时10x+5＝55．

答：该小学有5个班级，共有奥运福娃55套．

说明　列不等式组求解实际问题时一定要抓住题目中的关键性词语，寻找不等的关系式，从而构建不等式组．

4、(1)B(－3，0)；(2)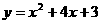或；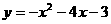

　 (3)在抛物线的对称轴上存在点P(－2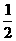，)，使△APE的周长最小。

本资料由《七彩教育网》 提供！

2、(1)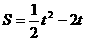；(2)10月；(3)5.5万元　 3、(1)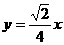；(2)－3≤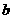≤0

4、如图，抛物线与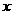轴的一个交点为A(－1，0)。

(1)求抛物线与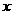轴的另一个交点B的坐标；

(2)D是抛物线与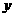轴的交点，C是抛物线上的一点，且以AB为一底的梯形ABCD的面积为9，求此抛物线的解析式；

(3)E是第二象限内到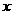轴、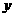轴的距离的比为5∶2的点，如果点E在(2)中的抛物线上，且它与点A在此抛物线对称轴的同侧。问：在抛物线的对称轴上是否存在点P，使△APE的周长最小？若存在，求出点P的坐标；若不存在，请说明理由。

3-3 二次函数(一)

3、抛物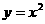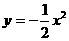线，和直线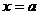(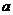＞0)分别交于A、B两点，已知∠AOB＝90⁰。

(1)求过原点O，把△AOB面积两等分的直线解析式；

(2)为使直线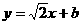与线段AB相交，那么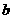值应是怎样的范围才适合？

2、某公司推出了一种高效环保型洗涤用品，年初上市后，公司经历了从亏损到盈利的过程。下面的二次函数图象(部分)刻画了该公司年初以来累积利润S(万元)与销售时间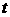(月)之间的关系(即前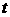个月的利润总和S与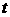之间的关系)。根据图象提供的信息，解答下列问题：

(1)由已知图象上的三点坐标，求累积利润S(万元)与时间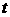(月)之间的函数关系式；

(2)求截止到几月末公司累积利润可达到30万元；

(3)求第8个月公司所获利润是多少万元？

1、已知函数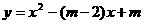的图像过点(－1，15)，设其图像与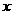轴交于点A、B，点C在图像上，且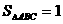，求点C的坐标。

4、已知抛物线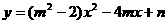的对称轴是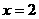，且它的最高点在直线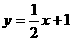上，则它的顶点为　　　　　 ，＝　　　　　 。