
题目列表(包括答案和解析)
4、 如图,直线
如图,直线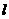 与
与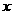 轴、
轴、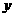 轴的正半轴分别交于A、B两点,且OA、OB的长是方程
轴的正半轴分别交于A、B两点,且OA、OB的长是方程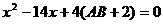 的两个根(OB>OA),P为直线
的两个根(OB>OA),P为直线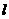 上A、B两点之间的一动点(不与A、B重合),PQ∥OB交OA于点Q。
上A、B两点之间的一动点(不与A、B重合),PQ∥OB交OA于点Q。
(1)求tan∠BAO的值;
(2)若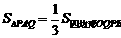 时,请确定点P在AB上的位置,并求出线段PQ的长。
时,请确定点P在AB上的位置,并求出线段PQ的长。
(3)在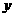 轴上是否存在点M,使△MPQ为等腰直角三角形。若存在,请直接写出点M的坐标,若不存在,请说明理由。
轴上是否存在点M,使△MPQ为等腰直角三角形。若存在,请直接写出点M的坐标,若不存在,请说明理由。
3-2 一次函数
3、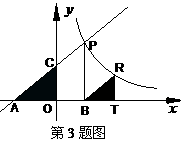 如图,直线
如图,直线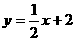 分别交
分别交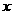 轴、
轴、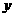 轴于A、C,P是该直线上在第一象限内的一点,PB⊥
轴于A、C,P是该直线上在第一象限内的一点,PB⊥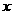 轴于B,
轴于B,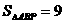 。
。
(1)求点P的坐标;
(2)设点R与点P在同一反比例函数的图像上,且点R在直线PB的右侧,作RT⊥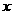 轴于T,当以B、R、T为顶点的三角形与△AOC相似时,求点R的坐标。
轴于T,当以B、R、T为顶点的三角形与△AOC相似时,求点R的坐标。
2、 如图,已知一次函数
如图,已知一次函数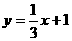 的图像与
的图像与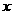 轴、
轴、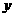 轴分别交于A、B两点,点C、D都在
轴分别交于A、B两点,点C、D都在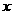 轴的正半轴上,D点坐标为(2,0),若两钝角∠ABD=∠BCD。
轴的正半轴上,D点坐标为(2,0),若两钝角∠ABD=∠BCD。
(1)求直线BC的解析式;
(2)若P是直线BD上一点,且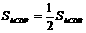 ,求P点坐标。
,求P点坐标。
1、一位投资者有两种选择:①中国银行发行五年期国债,年利率为2.63%。②中国人寿保险公司涪陵分公司推出的一种保险―鸿泰分红保险,投资者一次性交保费10000元(10份),保险期为5年,5年后可得本息和10486.60元,一般还可再分得一些红利,,但分红的金额不固定,有时可能多,有时可能少。
(1)写出购买国债的金额 (元)与5年后银行支付的本息和
(元)与5年后银行支付的本息和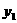 (元)的函数关系式;
(元)的函数关系式;
(2)求鸿泰分红保险的年利率,并写出支付保费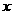 (元)与5年后保险公司还付的本息和
(元)与5年后保险公司还付的本息和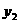 (元)的函数关系式(红利除外);
(元)的函数关系式(红利除外);
(3)请你帮助投资者分析两种投资的利弊。
3、如图,已知直线PA: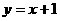 交
交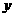 轴于Q,直线PB:
轴于Q,直线PB: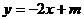 。若四边形PQOB的面积为
。若四边形PQOB的面积为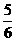 ,则
,则 = 。
= 。
 4、某气象研究中心观测一场沙尘暴从发生到结束的全过程,开始时风速平均每小时增加2千米,4小时后,沙尘暴经过开阔荒漠地,风速变为平均每小时增加4千米,一段时间风速保持不变,。当沙尘暴遇到绿色植被区时,其风速平均每小时减少1千米,最终停止。结合风速与时间的图像填空:
4、某气象研究中心观测一场沙尘暴从发生到结束的全过程,开始时风速平均每小时增加2千米,4小时后,沙尘暴经过开阔荒漠地,风速变为平均每小时增加4千米,一段时间风速保持不变,。当沙尘暴遇到绿色植被区时,其风速平均每小时减少1千米,最终停止。结合风速与时间的图像填空:
①在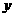 轴( )内填入相应的数值;
轴( )内填入相应的数值;
②沙尘暴从发生到结束共经过 小时;
③当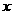 ≥25时,风速
≥25时,风速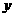 (千米/小时)与时间
(千米/小时)与时间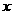 (小时)之间的函数关系式是 。
(小时)之间的函数关系式是 。
2、 一次函数
一次函数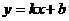 的图像经过点A(0,1),B(3,0),若将该图像沿着
的图像经过点A(0,1),B(3,0),若将该图像沿着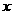 轴向左平移4个单位,则此图像沿
轴向左平移4个单位,则此图像沿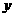 轴向下平移了
单位。
轴向下平移了
单位。
1、若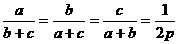 ,则直线
,则直线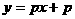 一定经过第 象限。
一定经过第 象限。
5、 小李以每千克0.80元的价格从批发市场购进若干千克西瓜到市场去销售,在销售了部分西瓜后余下的每千克降价0.40元,全部售完。销售金额与卖瓜的千克数之间的关系如图所示,那么小李赚( )
小李以每千克0.80元的价格从批发市场购进若干千克西瓜到市场去销售,在销售了部分西瓜后余下的每千克降价0.40元,全部售完。销售金额与卖瓜的千克数之间的关系如图所示,那么小李赚( )
A、32元 B、36元
C、38元 D、44元
4、直线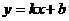 经过点A(-1,
经过点A(-1, )与点B(
)与点B( ,1),其中
,1),其中 >1,则必有( )
>1,则必有( )
A、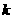 >0,
>0,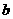 >0 B、
>0 B、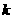 >0,
>0,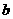 <0 C、
<0 C、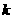 <0,
<0,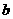 >0 D、
>0 D、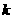 <0,
<0,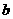 <0
<0
3、若一次函数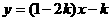 的图像不经过第二象限,则
的图像不经过第二象限,则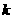 的取值范围是( )
的取值范围是( )
A、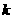 <
<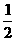 B、0<
B、0<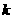 <
<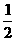 C、0≤
C、0≤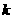 <
<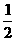 D、
D、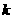 <0或
<0或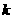 >
>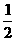
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com